
����Ŀ����ͼ1��OP����MON��ƽ���ߣ��������ø�ͼ�λ�һ����OP����ֱ��Ϊ�Գ����ȫ�������Σ��������ӵ�ȫ��������ע��ͼ�ϣ�
����ο������ȫ�������εķ���������������⣺
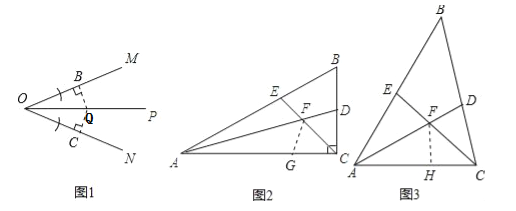
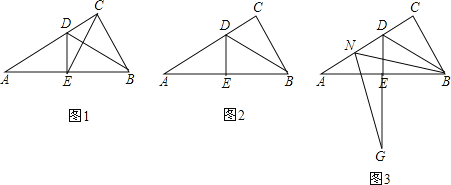
��1����ͼ2������ABC�У���ACB��ֱ�ǣ���B=60�㣬AD��CE�ֱ�����BAC����BCA��ƽ���ߣ�AD��CE�ཻ�ڵ�F������EFA�Ķ�����
��2���ڣ�1���������£����ж�FE��FD֮���������ϵ����˵�����ɣ�
��3����ͼ3������ABC�У������ACB����ֱ�ǣ����� 1 ���е������������䣬�����ڣ�2�������ý����Ƿ���Ȼ����������������֤����������������˵�����ɣ�

���𰸡���1��60����2��FE=FD��3��FE=FD��Ȼ����
��������
��OM��ON�Ϸֱ��ȡOB��OC��ʹOB=OC���ֱ����B��C��OM��ON�Ĵ��ߣ������߽��ڵ�Q������OQ�����OBQ�ա�OCQ����1����֪��A CB=90�㣬��B=60�������������ε��ڽǺͶ����������BAC=30�㣮����AD��CE�ֱ�����BAC����BCA��ƽ���ߣ����ݽ�ƽ���ߵĶ��������DAC=15�㣬��ECA=45�㣮������������ǵ����ʼ��������EFA=60�㣻��2��FE=FD����AC�Ͻ�ȡAG=AE��֤����EAF�ա�GAF�� ����ȫ�������ε����ʿɵ�FE=FG����EFA=��GFA=60�㣮��֤����DFC=��GFC������ASA�ж���FDC�ա�FGC���ɴ˿ɵ�FD=FG���Ӷ�֤�� FE=FD����3����2���еĽ���FE=FD��Ȼ������֤����ȣ�2���ķ������.
��ͼ��ʾ����OBQ�ա�OCQ��
��1����ͼ2���ߡ�ACB=90�㣬��B=60�㣮
���BAC=30�㣮
��AD��CE�ֱ�����BAC����BCA��ƽ���ߣ�
���DAC=![]() ��BAC=15�㣬��ECA=
��BAC=15�㣬��ECA=![]() ��ACB=45�㣮
��ACB=45�㣮
���EFA=��DAC+��ECA=15��+45��=60�㣮
��2��FE=FD��
��ͼ2����AC�Ͻ�ȡAG=AE������FG��
��AD����BAC��ƽ���ߣ�
���EAF=��GAF��
����EAF����GAF��
��
���EAF�ա�GAF��SAS����
��FE=FG����EFA=��GFA=60�㣮
���GFC=180�㩁60�㩁60��=60�㣮
���ߡ�DFC=��EFA=60�㣬
���DFC=��GFC��
����FDC����FGC��
��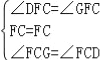
���FDC�ա�FGC��ASA����
��FD=FG��
��FE=FD��
��3����2���еĽ���FE=FD��Ȼ������
ͬ��2���ɵ���EAF�ա�HAF��
��FE=FH����EFA=��HFA��
���ɣ�1��֪��FAC=![]() ��BAC����FCA=
��BAC����FCA=![]() ��ACB��
��ACB��
���FAC+��FCA=![]() ����BAC+��ACB��=
����BAC+��ACB��=![]() =60�㣮
=60�㣮
���AFC=180�㩁����FAC+��FCA��=120�㣮
���EFA=��HFA=180�㩁120��=60�㣮
ͬ��2���ɵ���FDC�ա�FHC��
��FD=FH��
��FE=FD��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У��Խ���BD�Ĵ�ֱƽ����MN��AD�ཻ�ڵ�M����BD�ཻ�ڵ�O����BC�ཻ�ڵ�N������BM��DN��
��1����֤���ı���BMDN�����Σ�
��2����AB=4��AD=8��������BMDN������ͶԽ���MN�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪D��E�ֱ�Ϊ��ABC��AB��BC�ϵĶ��㣬ֱ��DE��ֱ��AC�ཻ��F����ADE��ƽ�������B��ƽ�����ཻ��P����ACB��ƽ�������F��ƽ�����ཻ��Q��
��1����ͼ1����F��AC����������ʱ�����P���Q֮���������ϵ��
��2����ͼ2����F��AC�ķ����ӳ�����ʱ�����P���Q֮���������ϵ���õ�ʽ��ʾ����
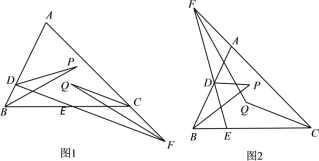
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��OEƽ����AOB��BD��OA�ڵ�D��AC��BO�ڵ�C����ͼ��ȫ�������ι���_______�ԣ�
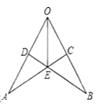
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������Ϊ����������ҵ�ķ�չ������ҵʵ���²������������ҵ�ľ�����
�����⡿����ij������ҵ2014 ��12�·ݲ�δ�����յ�700��Ԫ���²�������������2014 ��ľ���������ֻ��55%������������ʱ��λ����2014 ��ľ������������ﵽ60%��
��1����2013�����ҵ�������Ƕ�����Ԫ��
��2���־�ͳ�ƣ�2014��12�¸���ҵ�����²������¾�����Ϊ2100��Ԫ��2015��1�¼�2�²����²������¾�������������ӵİٷ����ֱ���m�� 2m���������µ��²�����ȣ��Ҷ���2014��12�»�����������2m�������㣬���Ժ���²����²������¾�������²������ȶ���2�·ݵ�ˮƽ���䣬�� 2015�����ҵ�����ﵽ2013���3������m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����֪AD��AE�ֱ��ǡ�ADC�͡�ABC�ĸߺ����ߣ�AB=6cm��AC=8cm��BC=10cm����CAB=90��������
��1��AD�ij���
��2����ABE�������
��3����ACE�͡�ABE���ܳ��IJ

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����AOB��45����AOB����һ����P����OP��10����OA����һ����Q��OB����һ����R������PQR�ܳ���С������С�ܳ��ǣ���

A. 10 B. ![]() C. 20 D.
C. 20 D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Rt��ABC�У���ACB=90������A=30����BD����ABC�Ľ�ƽ���ߣ�DE��AB�ڵ�E.
(1)��ͼ1������EC����֤����EBC�ǵȱ������Σ�
(2)��M���߶�CD�ϵ�һ��(�����C��D�غ�)����BMΪһ�ߣ���BM���·�����BMG=60����MG��DE�ӳ����ڵ�G.��֤��AD=DG+MD��
(3)��N���߶�AD�ϵ�һ�㣬��BNΪһ�ߣ���BN���·�����BNG=60����NG��DE�ӳ����ڵ�G.����ͼ3�л���ͼ�Σ���ֱ��д��ND��DG��AD����֮��Ĺ�ϵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABC�У���C=90�㣬AB=15��BC=9����P��Q�ֱ���BC��AC�ϣ�CP=3x��CQ=4x��0��x��3������D���߶�PQ�ϣ���PD=PC�� 
��1����֤��PQ��AB��
��2������D�ڡ�BAC��ƽ�����ϣ���CP�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com