
【题目】在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB于点E.
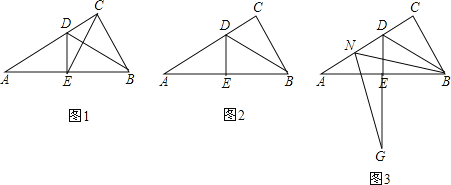
(1)如图1,连接EC,求证:△EBC是等边三角形;
(2)点M是线段CD上的一点(不与点C,D重合),以BM为一边,在BM的下方作∠BMG=60°,MG交DE延长线于点G.求证:AD=DG+MD;
(3)点N是线段AD上的一点,以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G.请在图3中画出图形,并直接写出ND,DG与AD数量之间的关系.
【答案】(1)证明见解析;(2)结论:AD=DG+DM,证明见解析;(3)结论:AD=DGDN.证明见解析.
【解析】
(1)、根据含有30°角的直角三角形的性质得出∠ABC=60°,BC=0.5AB,BE=0.5AB,从而得出等边三角形;(2)、延长ED使得DW=DM,连接MW,根据角平分线的性质以及直角三角形的性质得出△WDM是等边三角形,从而证明出△WGM和△DBM全等,得出答案;(3)、延长BD至H,使得DH=DN,利用直角三角形的性质证明出△DNG和△HNB全等,从而得出答案.
(1)证明:如图1所示: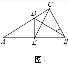
在Rt△ABC中,∠ACB=90°,∠A=30°,∴∠ABC=60°,BC=0.5AB;
∵BD平分∠ABC,∴∠1=∠DBA=∠A=30°.∴DA=DB.
∵DE⊥AB于点E ∴AE=BE=0.5AB,∴BC=BE, ∴△EBC是等边三角形;
(2)结论:AD=DG+DM.
证明:如图2所示:延长ED使得DW=DM,连接MW,
∵∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB于点E,
∴∠ADE=∠BDE=60°,AD=BD,又∵DM=DW, ∴△WDM是等边三角形,
∴MW=DM,∴△WGM≌△DBM,∴BD=WG=DG+DM,∴AD=DG+DM.
(3)结论:AD=DGDN.
证明:延长BD至H,使得DH=DN, 由(1)得DA=DB,∠A=30°.
∵DE⊥AB于点E, ∴∠2=∠3=60°,∴∠4=∠5=60°,∴△NDH是等边三角形
∴NH=ND ∠H=∠6=60°, ∴∠H=∠2, ∵∠BNG=60°,∴∠BNG+∠7=∠6+∠7.
即∠DNG=∠HNB, ∴△DNG≌△HNB(ASA), ∴DG=HB.
∵HB=HD+DB=ND+AD, ∴DG=ND+AD, ∴AD=DGND.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】如图,点0是等边△ABC内一点,∠AOB=110°,∠BOC=α,OC=CD,
且∠DOC=60°连接OD.
(1)求证:△COD是等边三角形
(2)当α=150°时,试判断△AOD的形状,并说明理由
(3)探究:当α为多少度时,△AOD是等腰三角形

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,OP是∠MON的平分线,请你利用该图形画一对以OP所在直线为对称轴的全等三角形,并将添加的全等条件标注在图上.
请你参考这个作全等三角形的方法,解答下列问题:
(1)如图2,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC和∠BCA的平分线,AD、CE相交于点F,求∠EFA的度数;
(2)在(1)的条件下,请判断FE与FD之间的数量关系,并说明理由;
(3)如图3,在△ABC中,如果∠ACB不是直角,而( 1 )中的其他条件不变,试问在(2)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,半径OA垂直于弦BC,垂足为E,点D在CA的延长线上,若∠DAB+
∠AOB=60°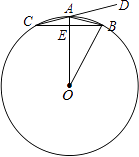
(1)求∠AOB的度数;
(2)若AE=1,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于抛物线y=ax2﹣4ax+3a下列说法:①对称轴为x=2;②抛物线与x轴两交点的坐标分别为(1,0),(3,0);③顶点坐标为(2,﹣a);④若a<0,当x>2时,函数y随x的增大而增大,其中正确的结论有( )个.
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学有一块四边形的空地ABCD,如图所示,为了绿化环境,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,DA=4m,BC=12m,CD=13m.
(1)求出空地ABCD的面积.
(2)若每种植1平方米草皮需要200元,问总共需投入多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=kx+b图象经过点(1,3)和(4,6)
①试求![]() 与
与![]() ;
;

②画出这个一次函数图象;
③这个一次函数与y轴交点坐标是( )
④当x 时,y<0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),A、E、F、C在一条直线上,AE=CF,过E、F分别作DE⊥AC,BF⊥AC,若AB=CD,试证明BD平分EF,若将△DEC的边EC沿AC方向移动变为图(2)时,其余条件不变,上述结论是否成立?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com