
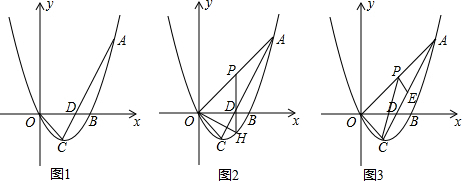
 Φ
Φ 分析 (1)把点A(3,3)和B(2,0)分别代入y=ax2+bx即可求出a、b的值;
(2)①设AO的解析式为y=kx,把A(3,3)代入解析式得到OA:y=x,设P(p,p),H(p,p2-2p),0<p<3,可得,PH=p-(p2-2p)=-p2+3p=-(p-$\frac{3}{2}$)2+$\frac{9}{4}$,据此即可求出PH取最大值$\frac{9}{4}$;②求出Q、P的坐标,求出PQ的方程为:$\frac{y-2}{p-2}$=$\frac{x-\frac{5}{2}}{p-\frac{5}{2}}$,即2(p-2)x-(2p-5)y-p=0,E与PQ的距离u=$\frac{|4(p-2)-(2p-5)-p|}{\sqrt{(2p-4)^{2}+(2p-5)^{2}}}$=$\frac{|p-3|}{\sqrt{8{p}^{2}-36p+41}}$;PC的方程为:$\frac{y+1}{p+1}$=$\frac{x-1}{p-1}$,(p+1)x-(p-1)y-2p=0,E与PQ的距离v=$\frac{\left|2(p+1)\right|-(p-1)-2p|}{\sqrt{(p+1)^{2}+(p-1)^{2}}}$=$\frac{|p-3|}{\sqrt{2{p}^{2}+2}}$,根据PE平分∠CPQ,得到u=v,8p2-36p+41=2p2+2,从而求出P的值,得到P的坐标,进而求出AP的长.
解答 解:(1)把点A(3,3)和B(2,0)分别代入y=ax2+bx得,
$\left\{\begin{array}{l}9a+3b=3\\ 4a+2b=0\end{array}\right.$,
解得,$\left\{\begin{array}{l}a=1\\ b=-2\end{array}\right.$.
(2)如图2,①设AO的解析式为y=kx,把A(3,3)代入解析式得,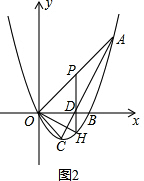
OA:y=x,
设P(p,p),H(p,p2-2p),0<p<3,
PH=p-(p2-2p)=-p2+3p=-(p-$\frac{3}{2}$)2+$\frac{9}{4}$,
p=$\frac{3}{2}$时,P($\frac{3}{2}$,$\frac{3}{2}$),PH取最大值$\frac{9}{4}$;
②由①得,y=x2-2x=x(x-2),
对称轴x=1,C(1,-1),E(2,1),
令C'P与AC的交点为Q.
△C'PQ与△CPA均含P为顶点,底都在AC上,即高相同.所以只需EQ的长为AC的$\frac{1}{4}$即可.
AC两点的横坐标之差为3-1=2,EQ两点的横坐标之差为2×$\frac{1}{4}$=$\frac{1}{2}$,Q的横坐标为2+$\frac{1}{2}$=$\frac{5}{2}$
AC:设AC解析式为y=mx+n,把C(1,-1),(3,3)分别代入解析式得,
$\left\{\begin{array}{l}m+n=-1\\ 3m+n=3\end{array}\right.$,
解得$\left\{\begin{array}{l}m=2\\ n=-3\end{array}\right.$,
可得函数解析式为y=2x-3,
∵Q($\frac{5}{2}$,2),
令P(p,p),
PQ的方程为:$\frac{y-2}{p-2}$=$\frac{x-\frac{5}{2}}{p-\frac{5}{2}}$,即2(p-2)x-(2p-5)y-p=0,
E与PQ的距离u=$\frac{|4(p-2)-(2p-5)-p|}{\sqrt{(2p-4)^{2}+(2p-5)^{2}}}$=$\frac{|p-3|}{\sqrt{8{p}^{2}-36p+41}}$;
PC的方程为:$\frac{y+1}{p+1}$=$\frac{x-1}{p-1}$,(p+1)x-(p-1)y-2p=0,
E与PQ的距离v=$\frac{\left|2(p+1)\right|-(p-1)-2p|}{\sqrt{(p+1)^{2}+(p-1)^{2}}}$=$\frac{|p-3|}{\sqrt{2{p}^{2}+2}}$,
PE平分∠CPQ,u=v,8p2-36p+41=2p2+2,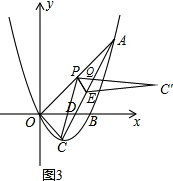
2p2-12p+13=0,
p=3-$\frac{\sqrt{3}}{2}$(另一根p=3+$\frac{\sqrt{3}}{2}$>3,舍去),
P(3-$\frac{\sqrt{3}}{2}$,3-$\frac{\sqrt{3}}{2}$),
OP=$\sqrt{(3-\frac{\sqrt{3}}{2})^{2}+(3-\frac{\sqrt{3}}{2})^{2}}$=3$\sqrt{2}$-$\frac{\sqrt{6}}{2}$,
AP=AO-OP=$\sqrt{{3}^{2}+{3}^{2}}$-(3$\sqrt{2}$-$\frac{\sqrt{6}}{2}$)=$\frac{\sqrt{6}}{2}$.
点评 本题是二次函数的综合题型,其中涉及到的知识点有抛物线的顶点公式和三角形的面积求法.待定系数法求二次函数解析式,求一次函数解析式,在翻折时,要注意翻折不变性.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:解答题
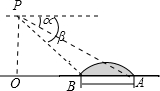 如图,直升飞机在跨河大桥AB的上方P点处,此时飞机离地面的高度PO=450m,且A、B、O三点在一条直线上,测得大桥两端的俯角分别为∠α=28°,∠β=43°,求大桥AB的长.(精确到1m)
如图,直升飞机在跨河大桥AB的上方P点处,此时飞机离地面的高度PO=450m,且A、B、O三点在一条直线上,测得大桥两端的俯角分别为∠α=28°,∠β=43°,求大桥AB的长.(精确到1m)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
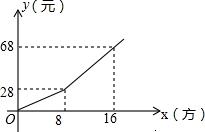 为鼓励市民节约用水,某市自来水公司按分段收费标准收费,如图反映的是每月所收水费y(元)与用水量x(方)之间的函数关系.
为鼓励市民节约用水,某市自来水公司按分段收费标准收费,如图反映的是每月所收水费y(元)与用水量x(方)之间的函数关系.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com