
【题目】四边形ABCD是正方形,PA是过正方形顶点A的直线,作DE⊥PA于E,将射线DE绕点D逆时针旋转45°与直线PA交于点F.
(1)如图1,当∠PAD=45°时,点F恰好与点A重合,则![]() 的值为 ;
的值为 ;
(2)如图2,若45°<∠PAD<90°,连接BF、BD,试求![]() 的值,并说明理由.
的值,并说明理由.

【答案】(1)![]() ;(2)
;(2)![]() =
=![]() .
.
【解析】
(1)由等腰直角三角形的性质可得AD=![]() AE,即可求解;
AE,即可求解;
(2)过点B作BH⊥AP于H,由“AAS”可证△ADE≌△BAH,可得AE=BH,由∠EFD=45°=∠ABD,可证点A,点F,点B,点D四点共圆,可得∠BFH=∠ADB=45°,即可求解.
(1)∵∠PAD=45°,DE⊥AP,
∴∠DAE=∠EDA,
∴AE=DE,
∴AD=![]() AE,
AE,
∵四边形ABCD是正方形,
∴AD=AB=BF=![]() AE,
AE,
∴![]() ;
;
(2)过点B作BH⊥AP于H,
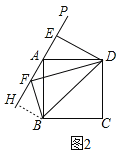
∵四边形ABCD是正方形,
∴AD=AB,∠ABD=45°,∠BAD=90°,
∴∠BAH+∠DAE=90°,
又∵∠BAH+∠ABH=90°,
∴∠ABH=∠DAE,
又∵AD=AB,∠DEA=∠AHB=90°,
∴△ADE≌△BAH(AAS),
∴AE=BH,
∵将射线DE绕点D逆时针旋转45°与直线PA交于点F,
∴∠EDF=45°,
∴∠EFD=45°=∠ABD,
∴点A,点F,点B,点D四点共圆,
∴∠BFH=∠ADB=45°,
又∵BH⊥AP,
∴∠FBH=∠BFH=45°,
∴BH=FH,
∴BF=![]() BH=
BH=![]() AE,
AE,
∴![]() =
=![]() =
=![]() .
.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
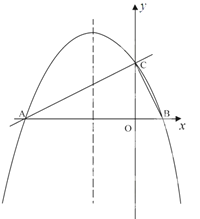
【题目】如图,在平面直角坐标系xoy中,直线![]() 与x 轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是
与x 轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是![]() 且经过A、C两点,与x轴的另一交点为点B.
且经过A、C两点,与x轴的另一交点为点B.
(1)①直接写出点B的坐标;②求抛物线解析式.
(2)若点P为直线AC上方的抛物线上的一点,连接PA,PC.求△PAC的面积的最大值,并求出此时点P的坐标.
(3)抛物线上是否存在点M,过点M作MN垂直x轴于点N,使得以点A、M、N为顶点的三角形与△ABC相似?若存在,直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】时下娱乐综艺节目风靡全国,随机对九年级部分学生进行了一次调查,对最喜欢《我是喜剧王》(记为A)、《王牌对王牌》(记为B)、《奔跑吧,兄弟》(记为C)、《欢乐喜剧人》(记为D)的同学进行了统计(每位同学只选择一个最喜欢的节目),绘制了以下不完整的统计图,请根据图中信息解答问题:
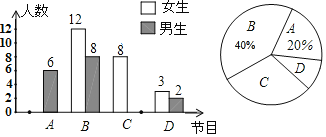
(1)求本次调查一共选取了多少名学生;
(2)将条形统计图补充完整;
(3)若九年级共有1900名学生,估计其中最喜欢《奔跑吧,兄弟》的学生大约是多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为阻断疫情向校园蔓延,确保师生生命安全和身体健康,教育部2020年1月29日下发通知,要求今年春季学期延期开学,“停课不停学”,统筹利用网络电视资源进行教学,某校为了让学生能够达到最佳的学习效果,确定老师们可以选用以下三种直播授课方式:A.智慧云直播,B.钉钉直播,C.腾讯会议直播.
(1)张明老师从三种网络授课方式中随机选取一种,是智慧云直播的概率为 ;
(2)张明和李刚两位老师从中随机各选取一种网络直播方式进行授课,请你用列表法或画树状图法,求出张明和李刚两位老师选取不同的网络直播授课方式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
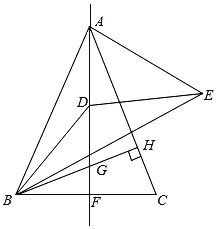
【题目】如图,在△ABC中,AB=AC=4,AF⊥BC于点F,BH⊥AC于点H.交AF于点G,点D在直线AF上运动,BD=DE,∠BDE=135°,∠ABH=45°,当AE取最小值时,BE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,经过原点的抛物线![]() 与直线
与直线![]() 交于
交于![]() ,
,![]() 两点,其对称轴是直线
两点,其对称轴是直线![]() ,抛物线与
,抛物线与![]() 轴的另一个交点为
轴的另一个交点为![]() ,线段
,线段![]() 与
与![]() 轴交于点
轴交于点![]() .
.
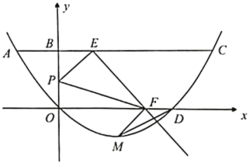
(1)求抛物线的解析式,并写出点![]() 的坐标;
的坐标;
(2)若点![]() 为线段
为线段![]() 上一点,且
上一点,且![]() ,点
,点![]() 为线段
为线段![]() 上不与端点重合的动点,连接
上不与端点重合的动点,连接![]() ,过点
,过点![]() 作直线
作直线![]() 的垂线交
的垂线交![]() 轴于点
轴于点![]() ,连接
,连接![]() ,探究在
,探究在![]() 点运动过程中,线段
点运动过程中,线段![]() ,
,![]() 有何数量关系?并证明所探究的结论;
有何数量关系?并证明所探究的结论;
(3)设抛物线顶点为![]() ,求当
,求当![]() 为何值时,
为何值时,![]() 为等腰三角形?
为等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某软件开发公司开发了A、B两种软件,每种软件成本均为1400元,售价分别为2000元、1800元,这两种软件每天的销售额共为112000元,总利润为28000元.
(1)该店每天销售这两种软件共多少个?
(2)根据市场行情,公司拟对A种软件降价销售,同时提高B种软件价格.此时发现,A种软件每降50元可多卖1件,B种软件每提高50元就少卖1件.如果这两种软件每天销售总件数不变,那么这两种软件一天的总利润最多是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com