
【题目】已知![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 边上一点,连接
边上一点,连接![]() ,
,![]() 是
是![]() 上一点,且
上一点,且![]() .
.
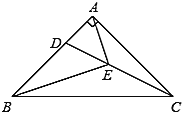
(1)如图1,若![]() ,
,
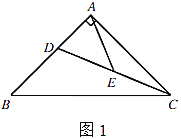
①求证:![]() 平分∠
平分∠![]() ;
;
②求![]() 的值;
的值;
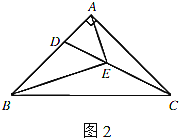
(2)如图2,连接![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
【答案】(1)①见解析,②![]() ;(2)
;(2)![]()
【解析】
(1)①先利用等腰三角形的性质求出![]() ,再得到
,再得到![]() ,故可知
,故可知![]() ,故可求解;
,故可求解;
②过点![]() 作
作![]() 于点
于点![]() ,根据
,根据![]() 平分
平分![]() ,得到
,得到![]() ,故
,故![]() ,利用特殊角的三角函数值即可求解;
,利用特殊角的三角函数值即可求解;
(2)证法一:过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,证明
,证明![]() ,得到
,得到![]() ,
,![]() ,再得到在
,再得到在![]() 和
和![]() 是等腰直角三角形,故
是等腰直角三角形,故![]() ,
,![]() ,再利用在
,再利用在![]() 中,
中,![]() 即可求解;
即可求解;
证法二:根据已知条件证明![]() ,得到
,得到![]() ,再利用在
,再利用在![]() 中,
中,![]() ,则
,则![]() ,从而得到
,从而得到![]() ,
,![]() ,再利用在
,再利用在![]() 中,
中,![]() 即可求解.
即可求解.
(1)①证明:∵![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() 平分
平分![]() .
.
②解:过点![]() 作
作![]() 于点
于点![]() ,
,
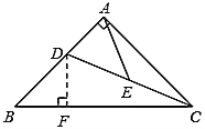
∴![]() .
.
∵![]() ,
,
∴![]() .
.
又![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)证法一:过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,
,
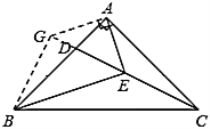
∴![]() .
.
又![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
![]() ,
,![]() ,
,
在![]() 中,
中,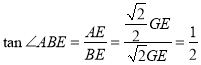 .
.
证法二:∵![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
在![]() 中,
中,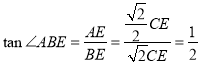 .
.


科目:初中数学 来源: 题型:
【题目】已知抛物线![]() ,与x轴交于两点A,B(点A在点B的左侧),与y轴交于点C.
,与x轴交于两点A,B(点A在点B的左侧),与y轴交于点C.
(Ⅰ)求点A,B和点C的坐标;
(Ⅱ)已知P是线段![]() 上的一个动点.
上的一个动点.
①若![]() 轴,交抛物线于点Q,当
轴,交抛物线于点Q,当![]() 取最大值时,求点P的坐标;
取最大值时,求点P的坐标;
②求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形,PA是过正方形顶点A的直线,作DE⊥PA于E,将射线DE绕点D逆时针旋转45°与直线PA交于点F.
(1)如图1,当∠PAD=45°时,点F恰好与点A重合,则![]() 的值为 ;
的值为 ;
(2)如图2,若45°<∠PAD<90°,连接BF、BD,试求![]() 的值,并说明理由.
的值,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为实现区域教育均衡发展,我市计划对某县![]() 、
、![]() 两类薄弱学校全部进行改造.根据预算,共需资金1575万元.改造一所
两类薄弱学校全部进行改造.根据预算,共需资金1575万元.改造一所![]() 类学校和两所
类学校和两所![]() 类学校共需资金230万元;改造两所
类学校共需资金230万元;改造两所![]() 类学校和一所
类学校和一所![]() 类学校共需资金205万元.
类学校共需资金205万元.
(1)改造一所![]() 类学校和一所
类学校和一所![]() 类学校所需的资金分别是多少万元?
类学校所需的资金分别是多少万元?
(2)若该县的![]() 类学校不超过5所,则
类学校不超过5所,则![]() 类学校至少有多少所?
类学校至少有多少所?
(3)我市计划今年对该县![]() 、
、![]() 两类学校共6所进行改造,改造资金由国家财政和地方财政共同承担.若今年国家财政拨付的改造资金不超过400万元;地方财政投入的改造资金不少于70万元,其中地方财政投入到
两类学校共6所进行改造,改造资金由国家财政和地方财政共同承担.若今年国家财政拨付的改造资金不超过400万元;地方财政投入的改造资金不少于70万元,其中地方财政投入到![]() 、
、![]() 两类学校的改造资金分别为每所10万元和15万元.请你通过计算求出有几种改造方案?
两类学校的改造资金分别为每所10万元和15万元.请你通过计算求出有几种改造方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,
中,![]() 的顶点
的顶点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 轴的负半轴上,
轴的负半轴上,![]() ,
,![]() 在反比例函数
在反比例函数![]() (
(![]() )的图象上,
)的图象上,![]() 与
与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,若
,若![]() 的面积是3,则
的面积是3,则![]() 的值是_________.
的值是_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】儿童用药的剂量常常按他们的体重来计算,某种药品,体重![]() 的儿童,每次正常服用量为
的儿童,每次正常服用量为![]() ;体重
;体重![]() 的儿童每次正常服用量为
的儿童每次正常服用量为![]() ;体重在
;体重在![]() 范围内时,每次正常服用量
范围内时,每次正常服用量![]() 是儿童体重
是儿童体重![]() 的一次函数中,现实中,该药品每次实际服用量可以比每次正常服用略高一些,但不能超过正常服用量的1.2倍,否则会对儿童的身体造成较大损害.
的一次函数中,现实中,该药品每次实际服用量可以比每次正常服用略高一些,但不能超过正常服用量的1.2倍,否则会对儿童的身体造成较大损害.
(1)求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)若该药品的一种包装规格为![]() /袋,求体重在什么范围的儿童生病时可以一次服下一袋药?
/袋,求体重在什么范围的儿童生病时可以一次服下一袋药?
查看答案和解析>>
科目:初中数学 来源: 题型:
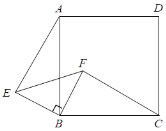
【题目】如图,△EBF为等腰直角三角形,点B为直角顶点, 四边形ABCD是正方形.
⑴ 求证:△ABE≌△CBF;
⑵ CF与AE有什么特殊的位置关系?请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
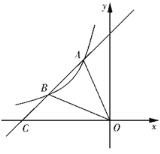
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图像交点A.点B,与x轴相交于点C,其中点A的坐标为(-2,4),点B的纵坐标为2.
的图像交点A.点B,与x轴相交于点C,其中点A的坐标为(-2,4),点B的纵坐标为2.
(1)当x为何值时,一次函数的值大于反比例函数的值.(直接写出来)
(2)求△AOB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com