练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，正方形ABCD的边长为4，分别以正方形的三边为直径在正方形内部作半圆，则阴影部分的面积之和是（　　）

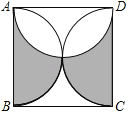
    A.8B.4C.16πD.4π

    【答案】A

    【解析】

    先判断出两半圆交点为正方形的中心，连接OA，OD，则可得出所产生的四个小弓形的面积相等，先得出2个小弓形的面积，即可求阴影部分面积．

    解：由题意，易知两半圆的交点即为正方形的中心，设此点为O，连接AO，DO，

    则图中的四个小弓形的面积相等，

    ∵两个小弓形面积＝S半圆AOD-S△AOD=S半圆AOD-S正方形ABCD，

    又正方形ABCD的边长为4，得各半圆的半径为2，

    ∴两个小弓形面积＝×π×22﹣×4×4=2π﹣4，

    ∴S阴影＝2×S半圆﹣4个小弓形面积＝π22﹣2（2π﹣4）＝8，

    故选：A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在直角坐标系中，点A的坐标为（0，8），点 B（b，t）在直线x=b上运动，点D、E、F分别为OB、0A、AB的中点，其中b是大于零的常数．

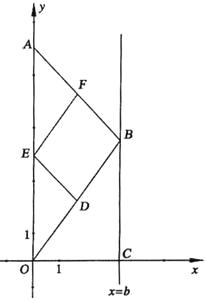
    （1）判断四边形DEFB的形状．并证明你的结论；

    （2）试求四边形DEFB的面积S与b的关系式；

    （3）设直线x=b与x轴交于点C，问：四边形DEFB能不能是矩形？若能．求出t的值；若不能，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

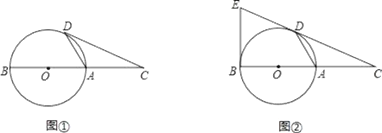
    【题目】已知点C为直径BA的延长线上一点，CD切⊙O于点D，

    （Ⅰ）如图①，若∠CDA=26°，求∠DAB的度数；

    （Ⅱ）如图②，过点B作⊙O的切线交CD的延长线于点E，若⊙O的半径为3，BC=10，求BE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】矩形纸片ABCD中，已知AD=8，AB=6，E是边BC上的点，以AE为折痕折叠纸片，使点B落在点F处，连接FC，当△EFC为直角三角形时，BE的长为　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

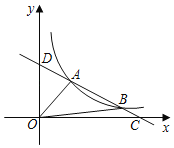
    【题目】如图，点A（m，3）、B（6，n）在双曲线y＝（x＞0）上，直线y＝ax+b经过A、B两点，并与x轴、y轴分别相交手C、D两点，已知S△OAB＝8．

    （1）求双曲线y＝的函数表达式；

    （2）求△COD的周长；

    （3）直接写出不等式-ax＞b的解集．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

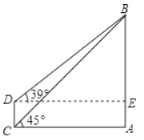
    【题目】目前世界上最高的电视塔是广州新电视塔．如图所示，新电视塔高AB为610米，远处有一栋大楼，某人在楼底C处测得塔顶B的仰角为45°，在楼顶D处测得塔顶B的仰角为39°．

    （1）求大楼与电视塔之间的距离AC；

    （2）求大楼的高度CD（精确到1米）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在中，以为直径的交于点，．

    （1）判断与的位置关系，并说明理由；

    （2）求证：；

    （3）在上取一点，若，，求的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知抛物线y＝ax2+bx+c经过A（﹣1，0）、B（5，0）、C（0，﹣5）三点．

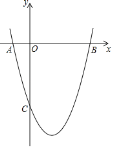
    （1）求抛物线的解析式和顶点坐标；

    （2）当0＜x＜5时，y的取值范围为　 　；

    （3）点P为抛物线上一点，若S△PAB＝21，直接写出点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】图1是一个地铁站入口的双翼闸机．如图2，它的双翼展开时，双翼边缘的端点A与B之间的距离为10cm，双翼的边缘AC＝BD＝54cm，且与闸机侧立面夹角∠PCA＝∠BDQ＝30°．当双翼收起时，可以通过闸机的物体的最大宽度为(　　)

    A. (54+10) cm B. (54+10) cm C. 64 cm D. 54cm

    查看答案和解析>>

    同步练习册答案