
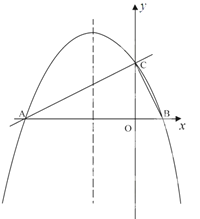
����Ŀ����ͼ����ƽ��ֱ������ϵxoy�У�ֱ��![]() ��x �ύ�ڵ�A����y�ύ�ڵ�C��������y=ax2+bx+c�ĶԳ�����
��x �ύ�ڵ�A����y�ύ�ڵ�C��������y=ax2+bx+c�ĶԳ�����![]() �Ҿ���A��C���㣬��x�����һ����Ϊ��B��
�Ҿ���A��C���㣬��x�����һ����Ϊ��B��
��1����ֱ��д����B�����ꣻ���������߽���ʽ��
��2������PΪֱ��AC�Ϸ����������ϵ�һ�㣬����PA��PC�����PAC����������ֵ���������ʱ��P�����꣮
��3�����������Ƿ���ڵ�M������M��MN��ֱx���ڵ�N��ʹ���Ե�A��M��NΪ��������������ABC���ƣ������ڣ�ֱ��д����M�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1����B��1,0����![]() ��2��4,P����2��3��;��3������M1��0��2��,M2����3,2��, M3��2����3��,M4��5����18��, ʹ���Ե� A��M��NΪ���������������ABC���ƣ�
��2��4,P����2��3��;��3������M1��0��2��,M2����3,2��, M3��2����3��,M4��5����18��, ʹ���Ե� A��M��NΪ���������������ABC���ƣ�
�������������������1���������ֱ��y=![]() x+2��x�ύ������꣬Ȼ�����������ߵĶԳ��Կ���õ�B�����ꣻ���������ߵĽ���ʽΪy=y=a��x+4����x��1����Ȼ��C��������뼴�����a��ֵ��
x+2��x�ύ������꣬Ȼ�����������ߵĶԳ��Կ���õ�B�����ꣻ���������ߵĽ���ʽΪy=y=a��x+4����x��1����Ȼ��C��������뼴�����a��ֵ��
��2�����P��Q�ĺ�����Ϊm���ֱ���õ�P��Q�������꣬�Ӷ��ɵõ��߶�PQ=-![]() m2��2m��Ȼ�����������ε������ʽ�����S��PAC=
m2��2m��Ȼ�����������ε������ʽ�����S��PAC=![]() ��PQ��4��Ȼ�������䷽���������PAC����������ֵ�Լ���ʱm��ֵ���Ӷ�����õ�P�����ꣻ
��PQ��4��Ȼ�������䷽���������PAC����������ֵ�Լ���ʱm��ֵ���Ӷ�����õ�P�����ꣻ
��3�����ȿ�֤����ABC�ס�ACO�ס�CBO��Ȼ������¼�������������ۼ��ɣ�����M����C���غϣ���M��0��2��ʱ����MAN�ס�BAC�������������ߵĶԳ��ԣ���M����3��2��ʱ����MAN�ס�ABC�� ������M�ڵ�������ʱ������ʱ����Ҫע�����������εĶ�Ӧ��ϵ��
�����������1����y=![]() x+2
x+2
��x=0ʱ��y=2����y=0ʱ��x=��4��
��C��0��2����A����4��0����
�������ߵĶԳ��Կ�֪����A���B����x=��![]() �Գƣ�
�Գƣ�
����B��������1��0����
�ڡ�������y=ax2+bx+c��A����4��0����B��1��0����
�����������߽���ʽΪy=a��x+4����x��1����
���������߹���C��0��2����
��2=��4a
��a=-![]()
��y=-![]() x2-
x2-![]() x+2��
x+2��
��2����P��m��-![]() m2-
m2-![]() m+2����
m+2����
����P��PQ��x�ύAC�ڵ�Q��
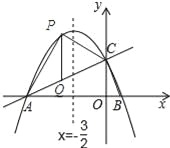
��Q��m��![]() m+2����
m+2����
��PQ=-![]() m2-
m2-![]() m+2����
m+2����![]() m+2��
m+2��
=-![]() m2��2m��
m2��2m��
��S��PAC=![]() ��PQ��4��
��PQ��4��
=2PQ=��m2��4m=����m+2��2+4��
����m=��2ʱ����PAC����������ֵ��4��
��ʱP����2��3����
��3����Rt��AOC��tan��CAO=![]() ��Rt��BOC��tan��BCO=
��Rt��BOC��tan��BCO=![]() ��
��
���CAO=��BCO��
�ߡ�BCO+��OBC=90����
���CAO+��OBC=90����
���ACB=90����
���ABC�ס�ACO�ס�CBO��
����ͼ��

����M����C���غϣ���M��0��2��ʱ����MAN�ס�BAC��
�� ���������ߵĶԳ��ԣ���M����3��2��ʱ����MAN�ס�ABC��
�� ����M�ڵ�������ʱ����M��n��-![]() n2-
n2-![]() n+2������N��n��0��
n+2������N��n��0��
��MN=![]() n2+
n2+![]() n��2��AN=n+4
n��2��AN=n+4
��![]() ʱ��MN=
ʱ��MN=![]() AN����
AN����![]() n2+
n2+![]() n��2=
n��2=![]() ��n+4��
��n+4��
�����ã�n2+2n��8=0
��ã�n1=��4���ᣩ��n2=2
��M��2����3����
��![]() ʱ��MN=2AN����
ʱ��MN=2AN����![]() n2+
n2+![]() n��2=2��n+4����
n��2=2��n+4����
�����ã�n2��n��20=0
��ã�n1=��4���ᣩ��n2=5��
��M��5����18����
��������������M1��0��2����M2����3��2����M3��2����3����M4��5����18����ʹ���Ե�A��M��NΪ���������������ABC���ƣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1Ϊ��ڵ����ϵ������ͼ2��ͼ3��������֧�ܵ�ʾ��ͼ��������֧������ͬ�����κ���ͬ�ĵ��������ι��ɣ�����E��H�ɷֱ��صȳ�������AB��DC�����ƶ���AF��EF��FG��1m��
��1�����ƶ�����ʹAE��EF�����AFE�Ķ��������BC�ij���
��2������AFE��60���Ϊ74��ʱ�������BC�����ӻ��Ǽ��٣����ӻ�����˶��٣��������ȷ��0.1m���ο����ݣ�![]() ��1.73��sin37���0.60��cos37���0.80��tan37���0.75��
��1.73��sin37���0.60��cos37���0.80��tan37���0.75��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
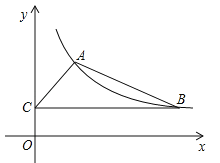
����Ŀ����ͼ��ij����������ͼ���һ֧������A��2��3���͵�B����B�ڵ�A���Ҳࣩ����BC��y�ᣬ����Ϊ��C������AB��AC��
��1����÷����������Ľ���ʽ��
��2������ABC�����Ϊ6����ֱ��AB�ı���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
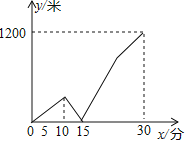
����Ŀ��һ���糿��С��Ӽҳ������ٲ��е�ѧУ��С�����һ��ʱ����������跢��С��������һ�������ѧϰ��Ʒ������������¥�����г�����С���н���·�ߣ�����ȥС�ᣬ������С�Ὣѧϰ��Ʒ����С���������ԭ·�����ٷ��ؼ��������·�����˽��࣬���践��ʱ�ﳵ���ٶ�ֻ��ԭ���ٶȵ�һ�룬С�������ԭ�ٶȲ���ǰ��ѧУ��������С��֮��ľ���y���ף���С��Ӽҳ������е�ʱ��x���֣�֮��Ĺ�ϵ��ͼ��ʾ��С��������ϡ���¥�Լ����轻ѧϰ��Ʒ��С�ᵢ���ʱ����Բ��ƣ���������ջص���ʱ��С����ѧУ�ľ���Ϊ_____�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ABC�Ķ��ǡ�A=36�㣨��ͼ����
��1�����ó߹���ͼ�����ǡ�ABC��ƽ����BD����AC�ڵ�D��������ͼ�ۼ�����Ҫ��д��������
��2��֤������ABC�ס�BDC��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���Գ���Ϊֱ��![]() �������߾���
�������߾���![]() ��
��![]() ���㣬��������
���㣬��������![]() �����һ����Ϊ
�����һ����Ϊ![]() ��
��
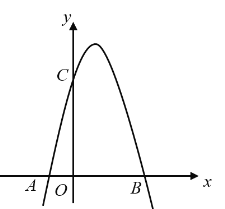
��1���������ߵĽ���ʽ��
��2������![]() Ϊ��һ��������������һ�㣬���ı���
Ϊ��һ��������������һ�㣬���ı���![]() �����Ϊ
�����Ϊ![]() ����
����![]() �����ֵ��
�����ֵ��
��3����![]() ���߶�
���߶�![]() ��һ���㣬��
��һ���㣬��![]() �����Ƿ���������ĵ�
�����Ƿ���������ĵ�![]() ��ʹ
��ʹ![]() Ϊ������������
Ϊ������������![]() Ϊֱ�������Σ������ڣ����
Ϊֱ�������Σ������ڣ����![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�������y����![]() x+3��x���һ������Ϊ��A����y��Ľ���Ϊ��B�������ߵĶԳ���l��x�ύ�ڵ㣬���߶�AB���ڵ�E����D�ǶԳ���l��һ���㣮
x+3��x���һ������Ϊ��A����y��Ľ���Ϊ��B�������ߵĶԳ���l��x�ύ�ڵ㣬���߶�AB���ڵ�E����D�ǶԳ���l��һ���㣮
��1����A���������� ������B���������� ����
��2���Ƿ���ڵ�D��ʹ�á�BDE�͡�ACE���ƣ������ڣ��������D�����꣬�������ڣ���˵�����ɣ�
��3����ͼ2�������ߵĶԳ���l����ƽ�����߶�AB���ڵ�F���������߽��ڵ�G�����ı���DEFG��ƽ���ı������ܳ����ʱ�������G�ĺ����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() ����x�ύ������A��B����A�ڵ�B����ࣩ����y�ύ�ڵ�C��
����x�ύ������A��B����A�ڵ�B����ࣩ����y�ύ�ڵ�C��
�������A��B�͵�C�����ꣻ
������֪P���߶�![]() �ϵ�һ�����㣮
�ϵ�һ�����㣮
����![]() �ᣬ���������ڵ�Q����
�ᣬ���������ڵ�Q����![]() ȡ���ֵʱ�����P�����ꣻ
ȡ���ֵʱ�����P�����ꣻ
����![]() ����Сֵ��
����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ı���ABCD�������Σ�PA�ǹ������ζ���A��ֱ�ߣ���DE��PA��E��������DE�Ƶ�D��ʱ����ת45����ֱ��PA���ڵ�F��
��1����ͼ1������PAD��45��ʱ����Fǡ�����A�غϣ���![]() ��ֵΪ�� ����
��ֵΪ�� ����
��2����ͼ2����45������PAD��90��������BF��BD������![]() ��ֵ����˵�����ɣ�
��ֵ����˵�����ɣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com