
【题目】如图,对称轴为直线![]() 的抛物线经过
的抛物线经过![]() ,
,![]() 两点,抛物线与
两点,抛物线与![]() 轴的另一交点为
轴的另一交点为![]() .
.
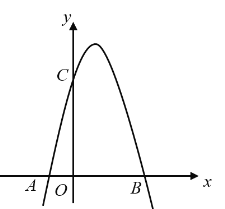
(1)求抛物线的解析式;
(2)若点![]() 为第一象限内抛物线上一点,设四边形
为第一象限内抛物线上一点,设四边形![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值;
的最大值;
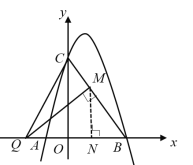
(3)若![]() 是线段
是线段![]() 上一动点,在
上一动点,在![]() 轴上是否存在这样的点
轴上是否存在这样的点![]() ,使
,使![]() 为等腰三角形且
为等腰三角形且![]() 为直角三角形?若存在,求出
为直角三角形?若存在,求出![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时,![]() ;(3)存在,
;(3)存在,![]() 点的坐标为
点的坐标为![]() 或
或![]() .
.
【解析】
(1)由对称轴的对称性得出点A的坐标,由待定系数法求出抛物线的解析式;
(2)作辅助线把四边形COBP分成梯形和直角三角形,表示出面积S,化简后是一个关于S的二次函数,求最值即可;
(3)分两种情况,当![]() 时,当
时,当![]() 时两种情况,结合相似三角形求解.
时两种情况,结合相似三角形求解.
解:(1)∵抛物线的对称轴为直线![]() ,
,![]() ,
,![]() 两点关于直线
两点关于直线![]() 对称且
对称且![]() ,
,
∴![]() .
.
∴设抛物线的解析式为![]() .
.
∵抛物线经过点![]() ,
,
∴![]() ,解得
,解得![]() .
.
∴抛物线的解析式为![]() ,
,
即![]() .
.
(2)如图,过点![]() 作
作![]() 于点
于点![]() .设
.设![]()
则![]() .
.
∴![]() ,
,![]() .
.
∴![]()
![]()
![]()
![]() .
.
∴当![]() 时,
时,![]() .
.
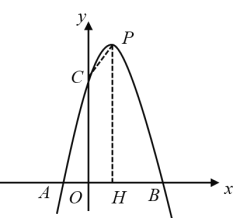
(3)分以下两种情况:
①如图所示:当![]() 时,
时,
∵![]() ,
,
∴只能![]() .
.
∵![]() ,
,![]() ,
,
设BC解析式为:y=kx+m,将B,C代入,
可得:k=-2,m=8,
∴直线![]() 的解析式为
的解析式为![]() .
.
设点![]() ,
,
则![]() ,
,![]() ,
,![]() .
.
在![]() 中,
中,
![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() ,即
,即![]() ,
,
![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() ,
,![]() .
.
∴![]() .
.
②如图所示:当![]() 时,
时,
∵![]() ,
,
∴只能![]() .
.
过点![]() 作
作![]() 轴于点
轴于点![]() ,
,
设点![]() ,
,
则![]() ,
,![]() ,
,![]() .
.
由①得:![]() ,
,![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
∴![]() ,即
,即![]()
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
∵![]() 轴于点
轴于点![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
∴![]() .
.
又∵![]() ,
,
∴![]()
∴![]() ,即
,即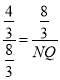 ,
,
∴![]()
∴![]() ,
,
∴![]() ,
,
综上所述,![]() 点的坐标为
点的坐标为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
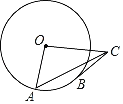
【题目】如图,⊙O的半径OA=2,B是⊙O上的动点(不与点A重合),过点B作⊙O的切线BC,BC=OA,连结OC,AC.当△OAC是直角三角形时,其斜边长为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
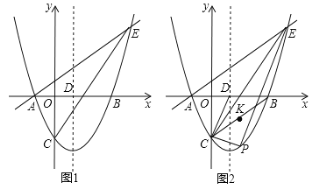
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,对称轴与
,对称轴与![]() 轴交于点
轴交于点![]() ,点
,点![]() 在抛物线上.
在抛物线上.
(1)求直线![]() 的解析式.
的解析式.
(2)点![]() 为直线
为直线![]() 下方抛物线上的一点,连接
下方抛物线上的一点,连接![]() ,
,![]() .当
.当![]() 的面积最大时,连接
的面积最大时,连接![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 的中点,点
的中点,点![]() 是线段
是线段![]() 上的一点,点
上的一点,点![]() 是线段
是线段![]() 上的一点,求
上的一点,求![]() 的最小值.
的最小值.
(3)点![]() 是线段
是线段![]() 的中点,将抛物线
的中点,将抛物线![]() 与
与![]() 轴正方向平移得到新抛物线
轴正方向平移得到新抛物线![]() ,
,![]() 经过点
经过点![]() ,
,![]() 的顶点为点
的顶点为点![]() ,在新抛物线
,在新抛物线![]() 的对称轴上,是否存在点
的对称轴上,是否存在点![]() ,使得
,使得![]() 为等腰三角形?若存在,直接写出点
为等腰三角形?若存在,直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
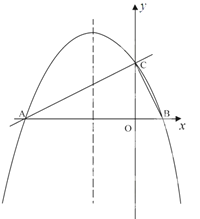
【题目】如图,在平面直角坐标系xoy中,直线![]() 与x 轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是
与x 轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是![]() 且经过A、C两点,与x轴的另一交点为点B.
且经过A、C两点,与x轴的另一交点为点B.
(1)①直接写出点B的坐标;②求抛物线解析式.
(2)若点P为直线AC上方的抛物线上的一点,连接PA,PC.求△PAC的面积的最大值,并求出此时点P的坐标.
(3)抛物线上是否存在点M,过点M作MN垂直x轴于点N,使得以点A、M、N为顶点的三角形与△ABC相似?若存在,直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为实现2020年全面脱贫的目标,我国实施“精准扶贫”战略,从而使贫困户的生活条件得到改善,生活质量明显提高.为了切实关注、关爱贫困家庭学生,某校对全校各班贫困家庭学生的人数情况进行了统计,统计发现班上贫困家庭学生人数分别有2名,3名,4名,5名,6名,共五种情况.并将其制成了如下两幅不完整的统计图:

请回答下列问题:
(1)求该校一共有班级________个;在扇形统计图中,贫困家庭学生人数有5名的班级所对应扇形圆心角为________°;
(2)将条形图补充完整;
(3)甲、乙、丙是贫困生中的三名学生,学校决定从这三名学生中随机抽取两名代表到市里进行发言,用列表法或画树状图法,求同时抽到甲,乙两名学生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
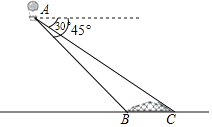
【题目】汉江是长江最长的支流,在历史上占居重要地位,陕西省境内的汉江为汉江上游段.李琳利用热气球探测器测量汉江某段河宽,如图,探测器在A处观测到正前方汉江两岸岸边的B、C两点,并测得B、C两点的俯角分别为45°,30°已知A处离地面的高度为80m,河平面BC与地面在同一水平面上,请你求出汉江该段河宽BC.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点![]() ,
,![]() 在反比例函数图象上,作直线
在反比例函数图象上,作直线![]() ,连接
,连接![]() 、
、![]() .
.
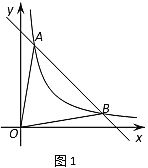
(1)求反比例函数的表达式和![]() 的值;
的值;
(2)求![]() 的面积;
的面积;
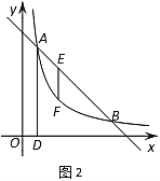
(3)如图2,![]() 是线段
是线段![]() 上一点,作
上一点,作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴的垂线,交反比例函数图象于点
轴的垂线,交反比例函数图象于点![]() ,若
,若![]() ,求出点
,求出点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com