
【题目】如图,![]() 中,
中,![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 逆时针旋转得
逆时针旋转得![]() ,当点
,当点![]() 落在
落在![]() 上时,
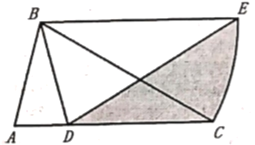
上时,![]() ,则阴影部分的面积为____.
,则阴影部分的面积为____.
【答案】![]()
【解析】
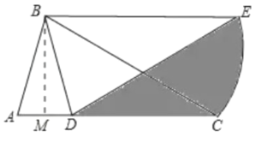
根据等腰三角形的性质和旋转的性质求得∠CBE=ABD=30°,根据平行线的性质求得∠ACB=∠CBE=30°,进而求得AB=AC=6,解直角三角形求得BM、MC,即可求得AD,由图形可知阴影部分的面积=△BDC的面积+扇形BCE的面积△ABC的面积,根据扇形面积公式和三角形面积公式计算即可.
解:∵∠A=75°,AB=AD,
∴∠ADB=∠A=75°,
∴∠ABD=180°2×75°=30°,
∴∠CBE=ABD=30°,
∵BE∥AC,
∴∠ACB=∠CBE=30°,
∴∠ABC=75°,
∴BC=AC=6,
作BM⊥AC于M,则AM=DM,
∴BM=![]() BC=3,MC=
BC=3,MC=![]() BC=3
BC=3![]() ,
,
∴AM=AC=MC=63![]() ,
,
∴AD=126![]() ,
,
由图形可知,阴影部分的面积=△BDC的面积+扇形BCE的面积△ABC的面积,
∴阴影部分的面积
=扇形BCE的面积△ABD的面积
=![]()
=![]() ,
,
故答案为: ![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
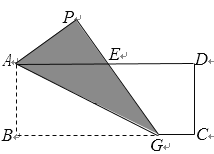
【题目】如图,矩形纸片ABCD中,AB=4,BC=10,G是BC边上一点,沿AG折叠△ABG,点B的落点为P,GP交AD于点E. 若E是AD的中点,则BG的长是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线![]() (
(![]() 为常数)交
为常数)交![]() 轴于点
轴于点![]() ,与
,与![]() 轴的一个交点在2和3之间,顶点为
轴的一个交点在2和3之间,顶点为![]() .
.
①抛物线![]() 与直线
与直线![]() 有且只有一个交点;
有且只有一个交点;
②若点![]() 、点
、点![]() 、点
、点![]() 在该函数图象上,则
在该函数图象上,则![]() ;
;
③将该抛物线向左平移2个单位,再向下平移2个单位,所得的抛物线解析式为![]() ;
;
④点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,点
,点![]() 、
、![]() 分别在
分别在![]() 轴和
轴和![]() 轴上,当
轴上,当![]() 时,四边形
时,四边形![]() 周长的最小值为
周长的最小值为![]() .
.
其中错误的是( )
A.①③B.②C.②④D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
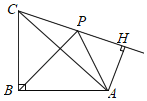
【题目】如图,等腰直角三角形ABC中,∠ABC=90°,BA=BC,将BC绕点B顺时针旋转θ(0°<θ<90°),得到BP,连结CP,过点A作AH⊥CP交CP的延长线于点H,连结AP,则∠PAH的度数( )
A.随着θ的增大而增大
B.随着θ的增大而减小
C.不变
D.随着θ的增大,先增大后减小
查看答案和解析>>
科目:初中数学 来源: 题型:
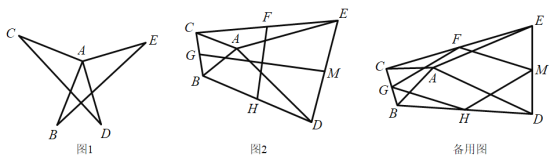
【题目】如图1为搭建在地面上的遮阳棚,图2、图3是遮阳棚支架的示意图.遮阳棚支架由相同的菱形和相同的等腰三角形构成,滑块E,H可分别沿等长的立柱AB,DC上下移动,AF=EF=FG=1m.
(1)若移动滑块使AE=EF,求∠AFE的度数和棚宽BC的长.
(2)当∠AFE由60°变为74°时,问棚宽BC是增加还是减少?增加或减少了多少?(结果精确到0.1m.参考数据:![]() ≈1.73,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
≈1.73,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,
,![]() (
(![]() ).
).
(1)观察猜想
如图1,当![]() 时,请直接写出线段
时,请直接写出线段![]() 与
与![]() 的数量关系: ;位置关系: ;
的数量关系: ;位置关系: ;
(2)类比探究
如图2,已知![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() ,
,![]() 的中点,写出
的中点,写出![]() 与
与![]() 的数量关系和位置关系,并说明理由;
的数量关系和位置关系,并说明理由;
(3)解决问题
如图,已知:![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() ,
,![]() 的中点,将
的中点,将![]() 绕点
绕点![]() 旋转,直接写出四边形
旋转,直接写出四边形![]() 的面积
的面积![]() 的范围(用含
的范围(用含![]() 的三角函数式子表示).
的三角函数式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
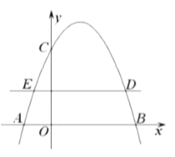
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() ,交抛物线于
,交抛物线于![]() 、
、![]() 两点.
两点.
(1)当![]() 时,求
时,求![]() ,
,![]() 两点的坐标;
两点的坐标;
(2)当![]() ,
,![]() 时,求抛物线的解析式;
时,求抛物线的解析式;
(3)当![]() 时,方程
时,方程![]() 在
在![]() 的范围内有实数解,请直接写出
的范围内有实数解,请直接写出![]() 的取值范围: .
的取值范围: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装公司招工广告承诺:熟练工人每月工资至少3000元.每天工作8小时,一个月工作25天.月工资底薪800元,另加计件工资.加工1件A型服装计酬16元,加工1件B型服装计酬12元.在工作中发现一名熟练工加工1件A型服装和2件B型服装需4小时,加工3件A型服装和1件B型服装需7小时.(工人月工资=底薪+计件工资)
(1)一名熟练工加工1件A型服装和1件B型服装各需要多少小时?
(2)一段时间后,公司规定:“每名工人每月必须加工A,B两种型号的服装,且加工A型服装数量不少于B型服装的一半”.设一名熟练工人每月加工A型服装a件,工资总额为W元.请你运用所学知识判断该公司在执行规定后是否违背了广告承诺?
查看答案和解析>>
科目:初中数学 来源: 题型:
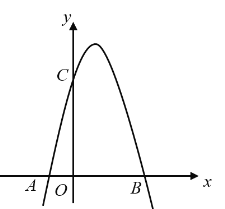
【题目】如图,对称轴为直线![]() 的抛物线经过
的抛物线经过![]() ,
,![]() 两点,抛物线与
两点,抛物线与![]() 轴的另一交点为
轴的另一交点为![]() .
.
(1)求抛物线的解析式;
(2)若点![]() 为第一象限内抛物线上一点,设四边形
为第一象限内抛物线上一点,设四边形![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值;
的最大值;
(3)若![]() 是线段
是线段![]() 上一动点,在
上一动点,在![]() 轴上是否存在这样的点
轴上是否存在这样的点![]() ,使
,使![]() 为等腰三角形且
为等腰三角形且![]() 为直角三角形?若存在,求出
为直角三角形?若存在,求出![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com