
【题目】若抛物线![]() (
(![]() 为常数)交
为常数)交![]() 轴于点
轴于点![]() ,与
,与![]() 轴的一个交点在2和3之间,顶点为
轴的一个交点在2和3之间,顶点为![]() .
.
①抛物线![]() 与直线
与直线![]() 有且只有一个交点;
有且只有一个交点;
②若点![]() 、点
、点![]() 、点
、点![]() 在该函数图象上,则
在该函数图象上,则![]() ;
;
③将该抛物线向左平移2个单位,再向下平移2个单位,所得的抛物线解析式为![]() ;
;
④点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,点
,点![]() 、
、![]() 分别在
分别在![]() 轴和
轴和![]() 轴上,当
轴上,当![]() 时,四边形
时,四边形![]() 周长的最小值为
周长的最小值为![]() .
.
其中错误的是( )
A.①③B.②C.②④D.③④
【答案】C
【解析】
①将![]() 代入
代入![]() 可得一元二次方程,利用
可得一元二次方程,利用![]() 判断方程根的情况可知交点个数;②由
判断方程根的情况可知交点个数;②由![]() 可知抛物线的对称轴,再利用抛物线的增减性判断即可;③根据平移公式即可求出平移后的解析式;④BC边一定,只要其余三边和最小,周长就最小,因此可作点B关于y轴的对称点
可知抛物线的对称轴,再利用抛物线的增减性判断即可;③根据平移公式即可求出平移后的解析式;④BC边一定,只要其余三边和最小,周长就最小,因此可作点B关于y轴的对称点![]() ,作点C关于x轴的对称点
,作点C关于x轴的对称点![]() ,连接
,连接![]() ,交x轴、y轴与点D、点E,此时
,交x轴、y轴与点D、点E,此时![]() 长即为三边和的最小值.
长即为三边和的最小值.
解:①将![]() 代入
代入![]() 得
得![]() ,即
,即![]() ,
,![]() ,所以此方程有2个相等的实数根,即抛物线
,所以此方程有2个相等的实数根,即抛物线![]() 与直线
与直线![]() 有且只有一个交点,①正确; ②抛物线的对称轴为
有且只有一个交点,①正确; ②抛物线的对称轴为![]() ,所以点
,所以点![]() 关于
关于![]() 的对称点为
的对称点为![]() ,
,![]() ,
,![]() 当
当![]() 时,y随x的增大而增大,又
时,y随x的增大而增大,又![]() ,②错误;③将该抛物线向左平移2个单位,再向下平移2个单位得
,②错误;③将该抛物线向左平移2个单位,再向下平移2个单位得![]() ,化简得
,化简得![]() ,即
,即![]() ,③正确;④当
,③正确;④当![]() 时,抛物线的解析式为
时,抛物线的解析式为![]() ,
,![]() ,
,![]() 点
点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,又因为BC边一定,所以其余三边和的最小值即当点
,又因为BC边一定,所以其余三边和的最小值即当点![]() 在一条直线上时取最小值,作点B关于y轴的对称点
在一条直线上时取最小值,作点B关于y轴的对称点![]() ,作点C关于x轴的对称点
,作点C关于x轴的对称点![]() ,连接
,连接![]() ,其余三边和的最小值即为
,其余三边和的最小值即为![]() 长,
长,

由两点间距离公式可得![]() ,
,![]() ,所以四边形
,所以四边形![]() 周长的最小值为
周长的最小值为![]() ,④错误.综上所述,错误的有②④.
,④错误.综上所述,错误的有②④.
故选:C.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】国家规定“中小学生每天在校体育活动时间不低于1小时”.为此,某市就“你每天在校体育活动时间是多少”的问题随机调查了辖区内300名初中学生.根据调查结果绘制成的统计图(部分)如图所示,其中分组情况是:
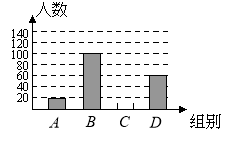
A组:![]() ;B组:
;B组:![]()
C组:![]() D组:
D组:![]()
请根据上述信息解答下列问题:
(1)C组的人数是;
(2)本次调查数据的中位数落在组内;
(3)若该辖区约有24 000名初中学生,请你估计其中达国家规定体育活动时间的人约有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某课题组为了解全市九年级学生对数学知识的掌握情况,在一次数学检测中,从全市16000名九年级考生中随机抽取部分学生的数学成绩进行调查,并将调查结果绘制成如下图表:
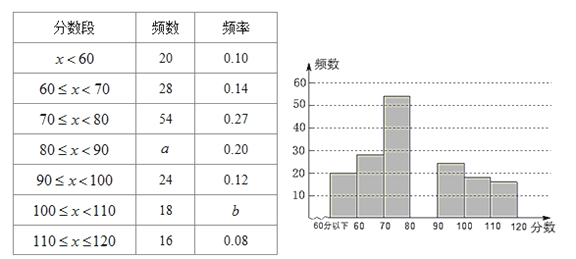
请根据以上图表提供的信息,解答下列问题:
(1)随机抽取部分学生的总人数是_________人,表格中的![]() _________.
_________.
(2)请补全频数分布直方图;
(3)如果把成绩在90分以上(含90分)定为优秀,那么该市16000名九年级考生数学成绩为优秀的学生约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某青春党支部在精准扶贫活动中,给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种.已知乙种树苗的价格比甲种树苗贵10元,用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同.
(1)求甲、乙两种树苗每棵的价格各是多少元?
(2)在实际帮扶中,他们决定再次购买甲、乙两种树苗共50棵,此时,甲种树苗的售价比第一次购买时降低了10%,乙种树苗的售价不变,如果再次购买两种树苗的总费用不超过1500元,那么他们最多可购买多少棵乙种树苗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年由于受“疫情”影响,某厂只能按用户的月需求量![]() (件)(
(件)(![]() )完成一种产品的生产,每件的售价为18万元,每件的成本
)完成一种产品的生产,每件的售价为18万元,每件的成本![]() (万元),
(万元),![]() 与
与![]() 的关系式为
的关系式为![]() (
(![]() ,
,![]() 为常数),经市场调研发现,月需求量
为常数),经市场调研发现,月需求量![]() 与月份
与月份![]() (
(![]() 为整数,
为整数,![]() )符合关系式
)符合关系式![]() (
(![]() 为常数),且得到下表中的数据.
为常数),且得到下表中的数据.

(1)求![]() 与
与![]() 满足的关系式;
满足的关系式;
(2)推断哪个月产品的需求量最小?最小为多少件?
(3)在这一年12个月中,若![]() 个月和第(
个月和第(![]() )个月的利润相差最大,求
)个月的利润相差最大,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 的网格中,
的网格中,![]() 均在格点上,请用无刻度的直尺作图(保留作图痕迹,不写作法).
均在格点上,请用无刻度的直尺作图(保留作图痕迹,不写作法).
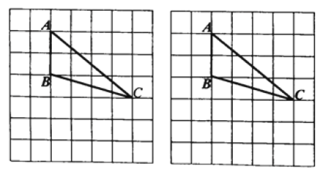
(1)在图1中找一格点![]() ,使得
,使得![]() 为等腰三角形(找到一个即可);
为等腰三角形(找到一个即可);
(2)在图2中作出![]() 的角平分线.
的角平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为了提高学生跳远科目的成绩,对全校500名九年级学生开展了为期一个月的跳远科目强化训练。王老师为了了解学生的训练情况,强化训练前,随机抽取了该年级部分学生进行跳远测试,经过一个月的强化训练后,再次测得这部分学生的跳远成绩,将两次测得的成绩制作成图所示的统计图和不完整的统计表(满分10分,得分均为整数).
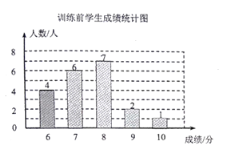
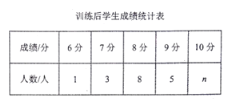
根据以上信息回答下列问题:
(1)训练后学生成绩统计表中![]() ,并补充完成下表:
,并补充完成下表:

(2)若跳远成绩9分及以上为优秀,估计该校九年级学生训练后比训练前达到优秀的人数增加了多少?
(3)经调查,经过训练后得到9分的五名同学中,有三名男生和两名女生,王老师要从这五名同学中随机抽取两名同学写出训练报告,请用列表或画树状图的方法,求所抽取的两名同学恰好是一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径OA=2,B是⊙O上的动点(不与点A重合),过点B作⊙O的切线BC,BC=OA,连结OC,AC.当△OAC是直角三角形时,其斜边长为__.
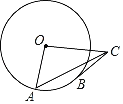
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com