
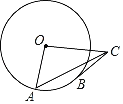
【题目】如图,⊙O的半径OA=2,B是⊙O上的动点(不与点A重合),过点B作⊙O的切线BC,BC=OA,连结OC,AC.当△OAC是直角三角形时,其斜边长为__.
科目:初中数学 来源: 题型:
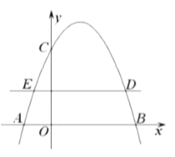
【题目】若抛物线![]() (
(![]() 为常数)交
为常数)交![]() 轴于点
轴于点![]() ,与
,与![]() 轴的一个交点在2和3之间,顶点为
轴的一个交点在2和3之间,顶点为![]() .
.
①抛物线![]() 与直线
与直线![]() 有且只有一个交点;
有且只有一个交点;
②若点![]() 、点
、点![]() 、点
、点![]() 在该函数图象上,则
在该函数图象上,则![]() ;
;
③将该抛物线向左平移2个单位,再向下平移2个单位,所得的抛物线解析式为![]() ;
;
④点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,点
,点![]() 、
、![]() 分别在
分别在![]() 轴和
轴和![]() 轴上,当
轴上,当![]() 时,四边形
时,四边形![]() 周长的最小值为
周长的最小值为![]() .
.
其中错误的是( )
A.①③B.②C.②④D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() ,交抛物线于
,交抛物线于![]() 、
、![]() 两点.
两点.
(1)当![]() 时,求
时,求![]() ,
,![]() 两点的坐标;
两点的坐标;
(2)当![]() ,
,![]() 时,求抛物线的解析式;
时,求抛物线的解析式;
(3)当![]() 时,方程
时,方程![]() 在
在![]() 的范围内有实数解,请直接写出
的范围内有实数解,请直接写出![]() 的取值范围: .
的取值范围: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装公司招工广告承诺:熟练工人每月工资至少3000元.每天工作8小时,一个月工作25天.月工资底薪800元,另加计件工资.加工1件A型服装计酬16元,加工1件B型服装计酬12元.在工作中发现一名熟练工加工1件A型服装和2件B型服装需4小时,加工3件A型服装和1件B型服装需7小时.(工人月工资=底薪+计件工资)
(1)一名熟练工加工1件A型服装和1件B型服装各需要多少小时?
(2)一段时间后,公司规定:“每名工人每月必须加工A,B两种型号的服装,且加工A型服装数量不少于B型服装的一半”.设一名熟练工人每月加工A型服装a件,工资总额为W元.请你运用所学知识判断该公司在执行规定后是否违背了广告承诺?
查看答案和解析>>
科目:初中数学 来源: 题型:
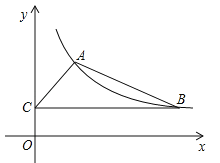
【题目】如图,某反比例函数图象的一支经过点A(2,3)和点B(点B在点A的右侧),作BC⊥y轴,垂足为点C,连结AB,AC.
(1)求该反比例函数的解析式;
(2)若△ABC的面积为6,求直线AB的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
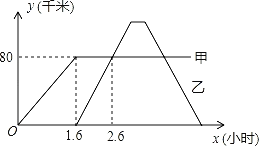
【题目】A,B两地相距200千米.早上8:00货车甲从A地出发将一批物资运往B地,行驶一段路程后出现故障,即刻停车与B地联系.B地收到消息后立即派货车乙从B地出发去接运甲车上的物资.货车乙遇到甲后,用了18分钟将物资从货车甲搬运到货车乙上,随后开往B地.两辆货车离开各自出发地的路程y(千米)与时间x(小时)的函数关系如图所示.(通话等其他时间忽略不计)
(1)求货车乙在遇到货车甲前,它离开出发地的路程y关于x的函数表达式.
(2)因实际需要,要求货车乙到达B地的时间比货车甲按原来的速度正常到达B地的时间最多晚1个小时,问货车乙返回B地的速度至少为每小时多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一天早晨,小玲从家出发匀速步行到学校,小玲出发一段时间后,她的妈妈发现小玲忘带了一件必需的学习用品,于是立即下楼骑自行车,沿小玲行进的路线,匀速去追小玲,妈妈追上小玲将学习用品交给小玲后,立即沿原路线匀速返回家里,但由于路上行人渐多,妈妈返回时骑车的速度只是原来速度的一半,小玲继续以原速度步行前往学校,妈妈与小玲之间的距离y(米)与小玲从家出发后步行的时间x(分)之间的关系如图所示(小玲和妈妈上、下楼以及妈妈交学习用品给小玲耽搁的时间忽略不计).当妈妈刚回到家时,小玲离学校的距离为_____米.
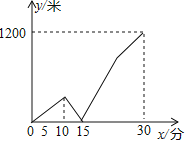
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对称轴为直线![]() 的抛物线经过
的抛物线经过![]() ,
,![]() 两点,抛物线与
两点,抛物线与![]() 轴的另一交点为
轴的另一交点为![]() .
.
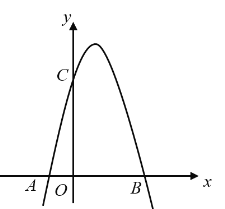
(1)求抛物线的解析式;
(2)若点![]() 为第一象限内抛物线上一点,设四边形
为第一象限内抛物线上一点,设四边形![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值;
的最大值;
(3)若![]() 是线段
是线段![]() 上一动点,在
上一动点,在![]() 轴上是否存在这样的点
轴上是否存在这样的点![]() ,使
,使![]() 为等腰三角形且
为等腰三角形且![]() 为直角三角形?若存在,求出
为直角三角形?若存在,求出![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com