
【题目】2015-2016赛季中国男子篮球职业联赛(即CBA)激战正酣,浙江广厦队表现不俗,暂居榜首,马布里领衔的卫冕冠军北京首钢队战绩不佳,截止12月23日,在前21轮比赛中,积35分位列第七位,按比赛规则,胜一场得2分,负一场得1分,那么截止12月23日北京首钢队共胜了多少场?
科目:初中数学 来源: 题型:
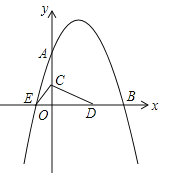
【题目】如图,已知抛物线![]() 与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
(1)直接写出抛物线的解析式: ;
(2)求△CED的面积S与D点运动时间t的函数解析式;当t为何值时,△CED的面积最大?最大面积是多少?
(3)当△CED的面积最大时,在抛物线上是否存在点P(点E除外),使△PCD的面积等于△CED的最大面积?若存在,求出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题提出】
用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
【问题探究】
不妨假设能搭成m种不同的等腰三角形,为探究m与n之间的关系,我们可以先从特殊入手,通过试验、观察、类比、最后归纳、猜测得出结论.
【探究一】
(1)用3根相同的木棒搭一个三角形,能搭成多少种不同的等腰三角形?
此时,显然能搭成一种等腰三角形.
所以,当n=3时,m=1.
(2)用4根相同的木棒搭一个三角形,能搭成多少种不同的等腰三角形?
只可分成1根木棒、1根木棒和2根木棒这一种情况,不能搭成三角形.
所以,当n=4时,m=0.
(3)用5根相同的木棒搭一个三角形,能搭成多少种不同的等腰三角形?
若分成1根木棒、1根木棒和3根木棒,则不能搭成三角形.
若分成2根木棒、2根木棒和1根木棒,则能搭成一种等腰三角形.
所以,当n=5时,m=1.
(4)用6根相同的木棒搭一个三角形,能搭成多少种不同的等腰三角形?
若分成1根木棒、1根木棒和4根木棒,则不能搭成三角形.
若分成2根木棒、2根木棒和2根木棒,则能搭成一种等腰三角形.
所以,当n=6时,m=1.
综上所述,可得:表①

【探究二】
(1)用7根相同的木棒搭一个三角形,能搭成多少种不同的三角形?
(仿照上述探究方法,写出解答过程,并将结果填在表②中)
(2)用8根、9根、10根相同的木棒搭一个三角形,能搭成多少种不同的等腰三角形?
(只需把结果填在表②中)
表②

你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究,…
【问题解决】:
用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?(设n分别等于4k﹣1,4k,4k+1,4k+2,其中k是正整数,把结果填在表③中)
表③

【问题应用】:
用2016根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?(写出解答过程),其中面积最大的等腰三角形每腰用了 根木棒.(只填结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题引入:
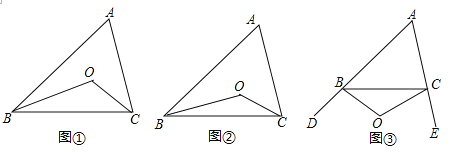
(1)如图①,在△ABC中,点O是∠ABC和∠ACB平分线的交点,若∠A=α,则∠BOC= (用α表示);如图②,∠CBO=![]() ∠ABC,∠BCO=
∠ABC,∠BCO=![]() ∠ACB,∠A=α,则∠BOC= (用α表示)
∠ACB,∠A=α,则∠BOC= (用α表示)
拓展研究:
(2)如图③,∠CBO=![]() ∠DBC,∠BCO=
∠DBC,∠BCO=![]() ∠ECB,∠A=α,请猜想∠BOC= (用α表示),并说明理由.
∠ECB,∠A=α,请猜想∠BOC= (用α表示),并说明理由.
类比研究:
(3)BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线,它们交于点O,∠CBO=![]() ∠DBC,∠BCO=
∠DBC,∠BCO=![]() ∠ECB,∠A=α,请猜想∠BOC= .
∠ECB,∠A=α,请猜想∠BOC= .
查看答案和解析>>
科目:初中数学 来源: 题型:
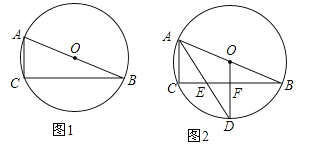
【题目】已知⊙O为△ABC的外接圆,圆心O在AB上.
(1)在图1中,用尺规作图作∠BAC的平分线AD交⊙O于D(保留作图痕迹,不写作法与证明);
(2)如图2,设∠BAC的平分线AD交BC于E,⊙O半径为5,AC=4,连接OD交BC于F.
①求证:OD⊥BC;
②求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小伟遇到这样一个问题:如图1,在△ABC(其中∠BAC是一个可以变化的角)中,AB=2,AC=4,以BC为边在BC的下方作等边△PBC,求AP的最大值.
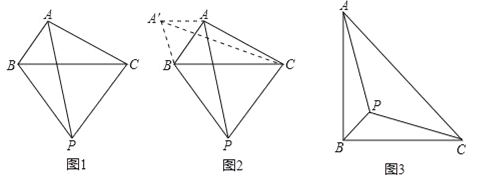
小伟是这样思考的:利用变换和等边三角形将边的位置重新组合.他的方法是以点B为旋转中心将△ABP逆时针旋转60°得到△A′BC,连接A′A,当点A落在A′C上时,此题可解(如图2).
(1)请你回答:AP的最大值是 .
(2)参考小伟同学思考问题的方法,解决下列问题:
如图3,等腰Rt△ABC.边AB=4,P为△ABC内部一点,请写出求AP+BP+CP的最小值长的解题思路.
提示:要解决AP+BP+CP的最小值问题,可仿照题目给出的做法.把△ABP绕B点逆时针旋转60,得到△A′BP′.
①请画出旋转后的图形
②请写出求AP+BP+CP的最小值的解题思路(结果可以不化简).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com