
【题目】如图,在平面直角坐标系![]() 中,过
中,过![]() 外一点
外一点![]() 引它的两条切线,切点分别为
引它的两条切线,切点分别为![]() ,
,![]() ,若
,若![]() ,则称
,则称![]() 为
为![]() 的环绕点.
的环绕点.
(1)当![]() 半径为1时,
半径为1时,
①在![]() ,
,![]() ,
,![]() 中,
中,![]() 的环绕点是_______________;
的环绕点是_______________;
②直线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() 轴交于点
轴交于点![]() ,若线段
,若线段![]() 上存在
上存在![]() 的环绕点,求
的环绕点,求![]() 的取值范围;
的取值范围;
(2)![]() 的半径为1,圆心为
的半径为1,圆心为![]() ,以
,以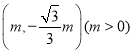 为圆心,
为圆心,![]() 为半径的所有圆构成图形
为半径的所有圆构成图形![]() ,若在图形
,若在图形![]() 上存在
上存在![]() 的环绕点,直接写出
的环绕点,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)①P1,P3;②![]() 或
或![]() ;(2)-2<t≤4
;(2)-2<t≤4
【解析】
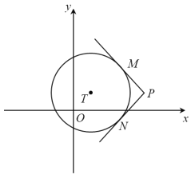
(1)①如图,PM,PN是⊙T的两条切线,M,N为切点,连接TM,TN.当∠MPN=60°时,可证TP=2TM,以T为圆心,TP为半径作⊙T,首先说明:当60°≤∠MPN<180°时,⊙T的环绕点在图中的圆环内部(包括大圆设的点不包括小圆上的点).利用这个结论解决问题即可.
②如图2中,设小圆交y轴的正半轴与于E.求出两种特殊位置b的值,结合图形根据对称性解决问题即可.
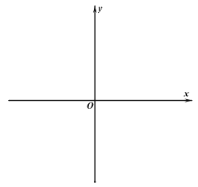
(2)如图3中,不妨设E(m,![]() m),则点E在直线y=
m),则点E在直线y=![]() x上,以E(m,
x上,以E(m,![]() m)(m>0)为圆心,
m)(m>0)为圆心,![]() m为半径的⊙E与x轴相切,作⊙E的切线ON,观察图象可知,以E(m,
m为半径的⊙E与x轴相切,作⊙E的切线ON,观察图象可知,以E(m,![]() m)(m>0)为圆心,
m)(m>0)为圆心,![]() m为半径的所有圆构成图形H,图形H即为∠MON的内部,包括射线OM,ON上.利用(1)中结论,画出圆环,当圆环与∠MON的内部有交点时,满足条件,求出两种特殊位置t的值即可解决问题.
m为半径的所有圆构成图形H,图形H即为∠MON的内部,包括射线OM,ON上.利用(1)中结论,画出圆环,当圆环与∠MON的内部有交点时,满足条件,求出两种特殊位置t的值即可解决问题.
(1)①如图,PM,PN是⊙T的两条切线,M,N为切点,连接TM,TN.
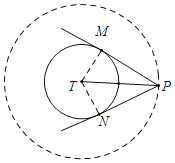
当∠MPN=60°时,∵PT平分∠MPN,
∵∠TPM=∠TPN=30°,
∵TM⊥PM,TN⊥PN,
∴∠PMT=∠PNT=90°,
∴TP=2TM,
以T为圆心,TP为半径作⊙T,
观察图象可知:当60°≤∠MPN<180°时,⊙T的环绕点在图中的圆环内部(包括大圆上的点不包括小圆上的点).
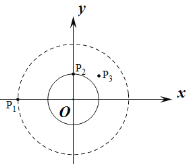
如图中,以O为圆心2为半径作⊙O,观察图象可知,P1,P3是⊙O的环绕点,
故答案为P1,P3.
②如图,设小圆交y轴的正半轴与于E.
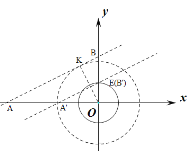
当直线![]() 经过点E时,b=1.
经过点E时,b=1.
当直线![]() 与大圆相切于K(在第二象限)时,连接OK,
与大圆相切于K(在第二象限)时,连接OK,
由题意B(0,b),A(-2b,0),
∴OB=b,OA=2b,![]() ,
,
∵OK=2,![]() ABOK=
ABOK=![]() OAOB,
OAOB,
∴![]() ,
,
解得![]() ,
,
观察图象可知,当![]() 时,线段AB上存在⊙O的环绕点,
时,线段AB上存在⊙O的环绕点,
根据对称性可知:当![]() 时,线段AB上存在⊙O的环绕点,
时,线段AB上存在⊙O的环绕点,
综上所述,满足条件的b的值为![]() 或
或![]() ;
;
(2)如图3中,不妨设E(m,![]() m),则点E在直线y=
m),则点E在直线y=![]() x上,
x上,
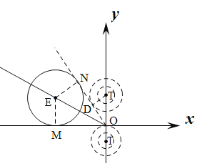
∵m>0,
∴点E在射线OE上运动,作EM⊥x轴,
∵E(m,![]() m),
m),
∴OM=m,EM=![]() ,
,
∴以E(m,![]() m)(m>0)为圆心,
m)(m>0)为圆心,![]() m为半径的⊙E与x轴相切,作⊙E的切线ON,观察图象可知,以E(m,
m为半径的⊙E与x轴相切,作⊙E的切线ON,观察图象可知,以E(m,![]() m)(m>0)为圆心,
m)(m>0)为圆心,![]() m为半径的所有圆构成图形H,图形H即为∠MON的内部,包括射线OM,ON上.
m为半径的所有圆构成图形H,图形H即为∠MON的内部,包括射线OM,ON上.
当⊙T的圆心在y轴的正半轴上时,假设以T为圆心,2为半径的圆与射线ON相切于D,连接TD.
∵![]() ,
,
∴∠EOM=30°,
∵ON,OM是⊙E的切线,
∴∠EON=∠EOM=30°,
∴∠TOD=30°,
∴OT=2DT=4,
∴T(0,4),
当⊙T的圆心在y轴的负半轴上时,且经过点O(0,0)时,T(0,-2),
观察图象可知,当-2<t≤4时,在图形H上存在⊙T的环绕点.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
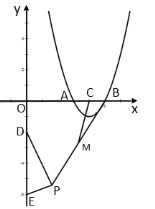
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,对称轴与
两点,对称轴与![]() 轴交于点
轴交于点![]() ,点
,点![]() ,点
,点![]() ,点
,点![]() 是平面内一动点,且满足
是平面内一动点,且满足![]() ,
,![]() 是线段
是线段![]() 的中点,连结
的中点,连结![]() .则线段
.则线段![]() 的最大值是( ).
的最大值是( ).
A.3B.![]() C.
C.![]() D.5
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数![]() 的图象记为
的图象记为![]() ,函数
,函数![]() 的图象记为
的图象记为![]() ,其中
,其中![]() 为常数,
为常数,![]() 与
与![]() 合起来的图象记为
合起来的图象记为![]() .
.
(Ⅰ)若![]() 过点
过点![]() 时,求
时,求![]() 的值;
的值;
(Ⅱ)若![]() 的顶点在直线
的顶点在直线![]() 上,求
上,求![]() 的值;
的值;
(Ⅲ)设![]() 在
在![]() 上最高点的纵坐标为
上最高点的纵坐标为![]() ,当
,当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年疫情防控期间.某小区卫生所决定购买A,B两种口罩.以满足小区居民的需要.若购买A种口罩9包,B种口罩4包,则需要700元;若购买A种口罩3包.B种口罩5包.则需要380元.
(1)购买人A,B两种口罩每包各需名少元?
(2)卫生所准备购进这两种口罩共90包,并且A种口罩包数不少于B种口罩包数的2倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线![]() 与双曲线
与双曲线![]() (x>0)交于点
(x>0)交于点![]() .
.
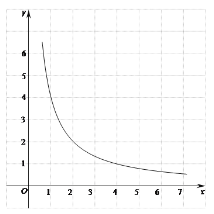
(1)求a,k的值;
(2)已知直线![]() 过点
过点![]() 且平行于直线
且平行于直线![]() ,点P(m,n)(m>3)是直线
,点P(m,n)(m>3)是直线![]() 上一动点,过点P分别作
上一动点,过点P分别作![]() 轴、
轴、![]() 轴的平行线,交双曲线
轴的平行线,交双曲线![]() (x>0)于点
(x>0)于点![]() 、
、![]() ,双曲线在点M、N之间的部分与线段PM、PN所围成的区域(不含边界)记为
,双曲线在点M、N之间的部分与线段PM、PN所围成的区域(不含边界)记为![]() .横、纵坐标都是整数的点叫做整点.
.横、纵坐标都是整数的点叫做整点.
①当![]() 时,直接写出区域
时,直接写出区域![]() 内的整点个数;②若区域
内的整点个数;②若区域![]() 内的整点个数不超过8个,结合图象,求m的取值范围.
内的整点个数不超过8个,结合图象,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 分别与x轴,y轴交于点
分别与x轴,y轴交于点![]() ,点C是第一象限内的一点,且
,点C是第一象限内的一点,且![]() ,抛物线
,抛物线![]() 经过
经过![]() 两点,与x轴的另一交点为D.
两点,与x轴的另一交点为D.
(1)求此抛物线的解析式;
(2)判断直线![]() 与
与![]() 的位置关系,并证明你的结论;
的位置关系,并证明你的结论;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以![]() 四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
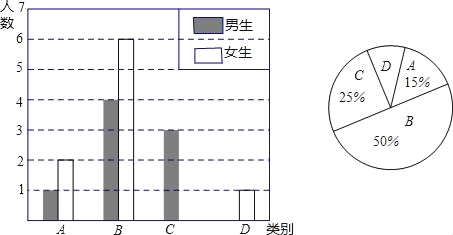
【题目】李老师为了了解班级学生自主学习、合作交流的具体情况,对九(1)班部分学生进行了为期半个月的跟踪调查,并将调查结果分成四类,A:特别好;B:好;C;一般;D:较差,并将调查结果绘制成以下两幅不完整的统计图.请你根据统计图解答下列问题:
(1)本次调查中,李老师一共调查了 名同学,其中女生共有 名.
(2)将上面的条形统计图补充完整;
(3)为了共同进步,李老师想从被调查的A类和D类学生中分别选取一位同学进行“一帮一”互助学习,请求所选两位同学恰好是一位男同学和一位女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
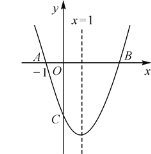
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴交于A,B两点,与y轴交于点C,且关于直线
轴交于A,B两点,与y轴交于点C,且关于直线![]() 对称,点A的坐标为(-1,0).
对称,点A的坐标为(-1,0).
(1)求二次函数的表达式;
(2)连接BC,若点P在y轴上时,BP和BC的夹角为15°,求线段CP的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某爱心组织筹集了部分资金,计划购买甲、乙两种救灾物品共2000件送往灾区,已知每件甲物品的价格比每件乙物品额价格贵10元,用350元购买甲种物品的件数恰好与用300元购买乙种物品的件数相同.
(1)求甲、乙两种救灾物品每件的价格是多少元?
(2)经调查,灾区对乙种物品件数的需求量是甲种物品件数的3倍,若该爱心组织按照此需求的比例购买这2000件物品,需筹集资金多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com