
����Ŀ����֪����ͼ���ڳ�����ABCD�У�AB=4��AD=6���ӳ�BC����E��ʹCE=3������DE��
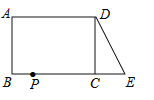
��1��DE�ij��� ����
��2������P�ӵ�B��������ÿ��1����λ���ٶ���BC��CD��DA���յ�A�˶������P�˶���ʱ��Ϊt�룬��tΪ��ֵʱ����ABP�͡�DCEȫ�ȣ�
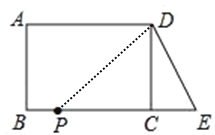
��3��������P�ӵ�B��������ÿ��1����λ���ٶȽ�����BE���յ�E�˶�������DP�����P�˶���ʱ��Ϊt�룬�Ƿ����t��ʹ��PDEΪ���������Σ������ڣ���ֱ��д��t��ֵ������˵�����ɣ�
���𰸡���1��5����2����tΪ3���13��ʱ����ABP����DCEȫ�ȣ���3��t��ֵΪ3��4��![]() ��
��
��������
��1�����ݾ��ε����ʿɵ�CD��4�����ݹ��ɶ�������DE�ij���
��2������ABP����DCEȫ�ȣ��ɵ�AP��CE��3��BP��CE��3������ʱ�䣽·�����ٶȣ�����t��ֵ��
��3����PD��DE��PE��DE��PD��PE����������ۣ��ֱ����õ��������ε����ʺ��ɶ������BP�����ɵõ�t��ֵ��
�⣺��1�����ı���ABCD�Ǿ��Σ�
��AB��CD��4��AD��BC��6��CD��BC��
��Rt��DCE��DE��![]() ��5��
��5��
�ʴ�Ϊ 5��
��2������ABP����DCEȫ�ȣ���BP��CE��AP��CE��
��BP��CE��3ʱ����t��![]() ��3�룬
��3�룬
��AP��CE��3ʱ����t��![]() ��13�룬
��13�룬
�൱tΪ3���13��ʱ����ABP����DCEȫ�ȣ�
��3������PDE������������PD��DE��PE��DE��PD��PE��
��PD��DEʱ��
��PD��DE��DC��BE��
��PC��CE��3��
��BP��BCPC��3��
��t��![]() ��3��
��3��
��PE��DE��5ʱ��
��BP��BEPE��
��BP��6+35��4��
��t��![]() ��4��
��4��
��PD��PEʱ��
��PE��PC��CE��3��PC��
��PD��3��PC��
��Rt��PDC��PD2��CD2��PC2��
�ࣨ3��PC��2��16��PC2��
��PC��![]() ��
��
��BP��BCPC��![]() ��
��
�� ��
��
����������t��ֵΪ3��4��![]() ��
��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У����κ���y=x2+bx+c��b��c���dz�������ͼ���㣨1��0���ͣ�0��2����
��1������2��x��2ʱ����y��ȡֵ��Χ��
��2����֪��P��m��n���ڸú�����ͼ���ϣ���m+n=1�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���֪AB=AC��AB�Ĵ�ֱƽ���߽�AB�ڵ�N����AC�ڵ�M������MB��
��1������ABC=70�������NMA�Ķ������� ���ȣ�
��2����AB=8cm����MBC���ܳ���14cm��
����BC�ij��ȣ�
������PΪֱ��MN��һ�㣬����ֱ��д����PBC�ܳ�����Сֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˽�ҳ������ӣ���ͨҲԽ��Խӵ����ͨ������£�ij�ι�·�ϳ�������ʻ�ٶȣ�ǧ��/ʱ����·��ÿ����ӵ�г�������x�������Ĺ�ϵ��ͼ��ʾ����x��8ʱ��y��x�ɷ�����������ϵ�������ٶȵ���20ǧ��/ʱ����ͨ�ͻ�ӵ�£�Ϊ������ֽ�ͨӵ�£���·��ÿ����ӵ�г�������xӦ������ķ�Χ�ǣ�������

A. x��32 B. x��32 C. x��32 D. x��32
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����ABCO�Ķ���OΪ����ԭ�㣬��CO��x���������ϣ���AOC=60��������������y=![]() ��x��0����ͼ����A�������ζԽ���BO�ڵ�D��DE��x���ڵ�E����CE��Ϊ��������
��x��0����ͼ����A�������ζԽ���BO�ڵ�D��DE��x���ڵ�E����CE��Ϊ��������

A. 1 B. ![]() C. 2
C. 2![]() ��
��![]() D.
D. ![]() ��1
��1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��y=k1x+b��x�ᡢy���ཻ��P��Q���㣬��y=![]() ��ͼ���ཻ��A����2��m����B��1��n�����㣬����OA��OB���������н��ۣ���k1k2��0����m+
��ͼ���ཻ��A����2��m����B��1��n�����㣬����OA��OB���������н��ۣ���k1k2��0����m+![]() n=0����S��AOP=S��BOQ���ܲ���ʽk1x+b>
n=0����S��AOP=S��BOQ���ܲ���ʽk1x+b>![]() �Ľ⼯��x����2��0��x��1��������ȷ�Ľ��۵������_____��
�Ľ⼯��x����2��0��x��1��������ȷ�Ľ��۵������_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ϣ�һ��أ���![]() ��
��![]() ��
��![]() ������ô
������ô![]() ������
������![]() ��
Ϊ��![]() �Ķ���������
�Ķ���������![]() ������ָ��ʽ
������ָ��ʽ![]() ����ת��Ϊ����ʽ
����ת��Ϊ����ʽ![]() ������ʽ
������ʽ![]() ����ת��Ϊָ��ʽ
����ת��Ϊָ��ʽ![]() ��
��
�������ϲ��ϣ�����������⣺
��1�����㣺![]() ��
��![]() ��
��![]() ��
��
��2���۲죨1���е����������²⣺![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����������֤�����������
����������֤�����������
��3����֪��![]() ����
����![]() ��
��![]() ��ֵ��
��ֵ��![]() ��
��![]() ����
����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ÿ��С�����εı߳�Ϊ1�ķ���ֽ�У��ѡ�ABC����ƽ��5������á�A1B1C1�����Ƶ�B1˳ʱ�뷽����ת90��á�A2B1C2.
��1������ƽ�ƺ���ת���ͼ�Σ���������Ӧ��ĸ.

��2������ӿ�ʼ��������������·���ij�.������ú��Це�ʽ�ӱ�ʾ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com