
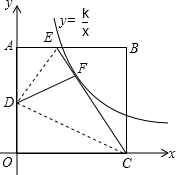
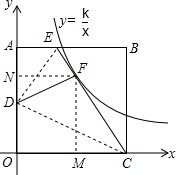
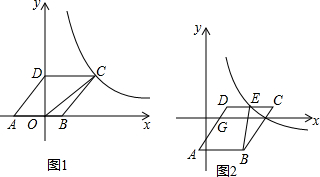
 如图,矩形ABCD的顶点O与直角坐标系的原点O重合,点A在y轴上,点C在x轴上,点E是AB边上一点,且BE=4,连接CE,把∠B沿CE对折,点B恰好落在线段AO上的点D处,把∠A沿DE对折,点A与CE线段上的点F重合,则过点F的反比例函数y=
如图,矩形ABCD的顶点O与直角坐标系的原点O重合,点A在y轴上,点C在x轴上,点E是AB边上一点,且BE=4,连接CE,把∠B沿CE对折,点B恰好落在线段AO上的点D处,把∠A沿DE对折,点A与CE线段上的点F重合,则过点F的反比例函数y=| k |
| x |
| 180 |
| 3 |
| ||
| 2 |
| 3 |
| 3 |
| ||
| 3 |
| 3 |
| ||
| 2 |
| BE |
| cos∠BEC |
| ||
| 2 |
5
| ||
| 2 |
5
| ||
| 2 |
| k |
| x |
15
| ||
| 2 |
15
| ||
| 2x |
15
| ||
| 2x |
| 180 |
| 3 |


科目:初中数学 来源: 题型:
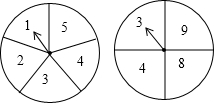 你喜欢转盘游戏吗?如图,图中的两个转盘分别被均匀地分成5个和4个扇形,每个扇形上都标有数字,同时自由转动两个转盘,转盘停止后,
你喜欢转盘游戏吗?如图,图中的两个转盘分别被均匀地分成5个和4个扇形,每个扇形上都标有数字,同时自由转动两个转盘,转盘停止后,查看答案和解析>>
科目:初中数学 来源: 题型:
 如图是我市环北路改造后一圆柱形输水管的横截面,阴影部分为有水部分,如果水面AB宽为4m,水面最深地方的高度为1m,则该输水管的半径为( )
如图是我市环北路改造后一圆柱形输水管的横截面,阴影部分为有水部分,如果水面AB宽为4m,水面最深地方的高度为1m,则该输水管的半径为( )| A、2m | B、2.5m |
| C、4m | D、5m |
查看答案和解析>>
科目:初中数学 来源: 题型:
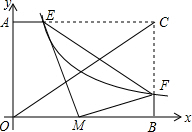 如图,在平面直角坐标系中,矩形AOBC的边OA,OB分别在y轴和x轴上,已知对角线OC=5,tan∠BOC=
如图,在平面直角坐标系中,矩形AOBC的边OA,OB分别在y轴和x轴上,已知对角线OC=5,tan∠BOC=| 3 |
| 4 |
| k |
| x |
| A、2 | ||
B、
| ||
| C、3 | ||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
| k |
| x |
| k |
| x |
| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
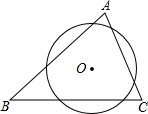 如图所示,在△ABC中,∠A=70°,⊙O截△ABC的三条边所得的弦长相等,则∠BOC的度数为( )
如图所示,在△ABC中,∠A=70°,⊙O截△ABC的三条边所得的弦长相等,则∠BOC的度数为( )| A、125° | B、130° |
| C、135° | D、160° |
查看答案和解析>>
科目:初中数学 来源: 题型:
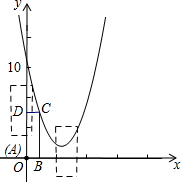 在直角坐标系中,抛物线y=x2+bx+c经过点(0,10)和点(4,2).
在直角坐标系中,抛物线y=x2+bx+c经过点(0,10)和点(4,2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com