
【题目】如图①,四边形![]() 是知形,
是知形,![]() ,点
,点![]() 是线段
是线段![]() 上一动点(不与
上一动点(不与![]() 重合),点
重合),点![]() 是线段
是线段![]() 延长线上一动点,连接
延长线上一动点,连接![]() 交
交![]() 于点
于点![]() .设
.设![]() ,已知
,已知![]() 与
与![]() 之间的函数关系如图②所示.
之间的函数关系如图②所示.
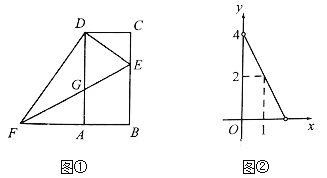
(1)求图②中![]() 与
与![]() 的函数表达式;
的函数表达式;
(2)求证:![]() ;
;
(3)是否存在![]() 的值,使得
的值,使得![]() 是等腰三角形?如果存在,求出
是等腰三角形?如果存在,求出![]() 的值;如果不存在,说明理由
的值;如果不存在,说明理由
【答案】(1)y=﹣2x+4(0<x<2);(2)见解析;(3)存在,x=![]() 或
或![]() 或
或![]() .
.
【解析】
(1)利用待定系数法可得y与x的函数表达式;
(2)证明△CDE∽△ADF,得∠ADF=∠CDE,可得结论;
(3)分三种情况:
①若DE=DG,则∠DGE=∠DEG,
②若DE=EG,如图①,作EH∥CD,交AD于H,
③若DG=EG,则∠GDE=∠GED,
分别列方程计算可得结论.
(1)设y=kx+b,
由图象得:当x=1时,y=2,当x=0时,y=4,
代入得:![]() ,得
,得![]() ,
,
∴y=﹣2x+4(0<x<2);
(2)∵BE=x,BC=2
∴CE=2﹣x,
∴![]() ,
,
∴![]() ,
,
∵四边形ABCD是矩形,
∴∠C=∠DAF=90°,
∴△CDE∽△ADF,
∴∠ADF=∠CDE,
∴∠ADF+∠EDG=∠CDE+∠EDG=90°,
∴DE⊥DF;
(3)假设存在x的值,使得△DEG是等腰三角形,
①若DE=DG,则∠DGE=∠DEG,
∵四边形ABCD是矩形,
∴AD∥BC,∠B=90°,
∴∠DGE=∠GEB,
∴∠DEG=∠BEG,
在△DEF和△BEF中,
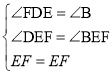 ,
,
∴△DEF≌△BEF(AAS),
∴DE=BE=x,CE=2﹣x,
∴在Rt△CDE中,由勾股定理得:1+(2﹣x)2=x2,
x=![]() ;
;
②若DE=EG,如图①,作EH∥CD,交AD于H,
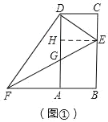
∵AD∥BC,EH∥CD,
∴四边形CDHE是平行四边形,
∴∠C=90°,
∴四边形CDHE是矩形,
∴EH=CD=1,DH=CE=2﹣x,EH⊥DG,
∴HG=DH=2﹣x,
∴AG=2x﹣2,
∵EH∥CD,DC∥AB,
∴EH∥AF,
∴△EHG∽△FAG,
∴![]() ,
,
∴![]() ,
,
∴![]() (舍),
(舍),
③若DG=EG,则∠GDE=∠GED,
∵AD∥BC,
∴∠GDE=∠DEC,
∴∠GED=∠DEC,
∵∠C=∠EDF=90°,
∴△CDE∽△DFE,
∴![]() ,
,
∵△CDE∽△ADF,
∴![]() ,
,
∴![]() ,
,
∴2﹣x=![]() ,x=
,x=![]() ,
,
综上,x=![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
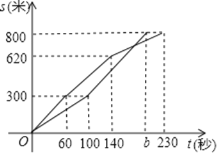
【题目】某校初三年级进行女子800米测试,甲、乙两名同学同时起跑,甲同学先以a米/秒的速度匀速跑,一段时间后提高速度,以![]() 米/秒的速度匀速跑,b秒到达终点,乙同学在第60秒和第140秒时分别减慢了速度,设甲、乙两名同学所的路程为s(米),乙同学所用的时间为t(秒),s与t之间的函数图象如图所示.
米/秒的速度匀速跑,b秒到达终点,乙同学在第60秒和第140秒时分别减慢了速度,设甲、乙两名同学所的路程为s(米),乙同学所用的时间为t(秒),s与t之间的函数图象如图所示.
(1)乙同学起跑的速度为______米/秒;
(2)求a、b的值;
(3)当乙同学领先甲同学60米时,直接写出t的值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
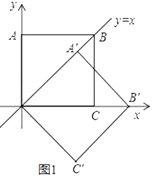
【题目】在平面直角坐标系中,O为原点,边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,现将正方形OABC绕点O顺时针旋转.
(1)如图①,当点A的对应的A′落在直线y=x上时,点A′的对应坐标为________;点B的对应点B′的坐标为_________;
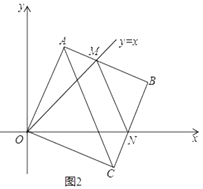
(2)旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N,当A点第一次落在直线y=x上时,停止旋转.
①如图2,在正方形OABC旋转过程中,线段AM,MN,NC三者满足什么样的数量关系?请说明理由;
②当AC∥MN时,求△MBN内切圆的半径(直接写出结果即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
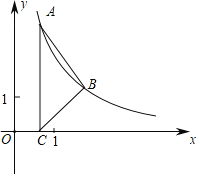
【题目】如图,在平面直角坐标系中,双曲线l:y=![]() (x>0)过点A(a,b),B(2,1)(0<a<2);过点A作AC⊥x轴,垂足为C.
(x>0)过点A(a,b),B(2,1)(0<a<2);过点A作AC⊥x轴,垂足为C.
(1)求l的解析式;
(2)当△ABC的面积为2时,求点A的坐标;
(3)点P为l上一段曲线AB(包括A,B两点)的动点,直线l1:y=mx+1过点P;在(2)的条件下,若y=mx+1具有y随x增大而增大的特点,请直接写出m的取值范围.(不必说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,O是对角线BD的中点,过点O的直线EF分别交DA,BC的延长线于E,F.
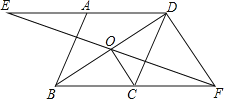
(1)求证:AE=CF;
(2)若AE=BC,试探究线段OC与线段DF之间的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知平面内有一个△ABC,O为平面内的一点,延长AO到A′,使OA′=OA,延长BO到B′,使OB′=OB,延长CO到从C′,使OC′=OC,得到△A′B′C′,问:△A′B′C′与△ABC是否全等?这两个三角形的对应边是否平行?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
材料1:在处理分数和分式问题时,有时由于分子比分母大,或者分子的次数高于分母的次数,在实际运算时往往难度比较大,这时我们可以将假分数(分式)拆分成一个整数(整式)与一个真分数(式)的和(差)的形式,通过对简单式的分析来解决问题,我们称之为分离整数法.此法在处理分式或整除问题时颇为有效.
例:将分式![]() 拆分成一个整式与一个分式(分子为整数)的和的形式.
拆分成一个整式与一个分式(分子为整数)的和的形式.
解:设x+2=t,则x=t﹣2.
∴原式=![]()
∴![]()
这样,分式![]() 就拆分成一个整式(x﹣5)与一个分式
就拆分成一个整式(x﹣5)与一个分式![]() 的和的形式.
的和的形式.
根据以上阅读材料回答下列问题:
(1)将分式![]() 拆分成一个整式与一个分子为整数的分式的和的形式,则结果为 ;
拆分成一个整式与一个分子为整数的分式的和的形式,则结果为 ;
(2)已知分式![]() 的值为整数,求整数x的值;
的值为整数,求整数x的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在Rt△ABC中,∠BAC=90°,CD为∠ACB的平分线,将∠ACB沿CD所在的直线对折,使点B落在点B′处,连结AB',BB',延长CD交BB'于点E,设∠ABC=2α(0°<α<45°).
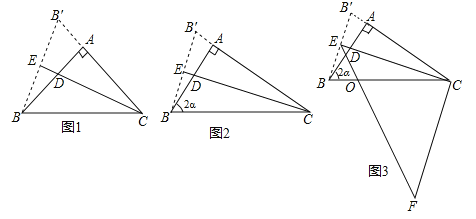
(1)如图1,若AB=AC,求证:CD=2BE;
(2)如图2,若AB≠AC,试求CD与BE的数量关系(用含α的式子表示);
(3)如图3,将(2)中的线段BC绕点C逆时针旋转角(α+45°),得到线段FC,连结EF交BC于点O,设△COE的面积为S1,△COF的面积为S2,求![]() (用含α的式子表示).
(用含α的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线y=ax2+bx+3(a≠0)与x轴分别交于A(﹣3,0),B两点,与y轴交于点C,抛物线的顶点E(﹣1,4),对称轴交x轴于点F.
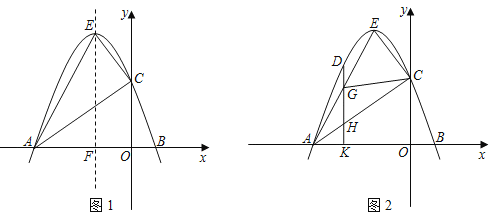
(1)请直接写出这条抛物线和直线AE、直线AC的解析式;
(2)连接AC、AE、CE,判断△ACE的形状,并说明理由;
(3)如图2,点D是抛物线上一动点,它的横坐标为m,且﹣3<m<﹣1,过点D作DK⊥x轴于点K,DK分别交线段AE、AC于点G、H.在点D的运动过程中,
①DG、GH、HK这三条线段能否相等?若相等,请求出点D的坐标;若不相等,请说明理由;
②在①的条件下,判断CG与AE的数量关系,并直接写出结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com