
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�������y��ax2+bx+3��a��0����x��ֱ���A����3��0����B���㣬��y�ύ�ڵ�C�������ߵĶ���E����1��4�����Գ��ύx���ڵ�F��
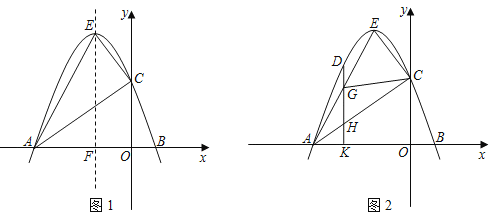
��1����ֱ��д�����������ߺ�ֱ��AE��ֱ��AC�Ľ���ʽ��
��2������AC��AE��CE���жϡ�ACE����״����˵�����ɣ�
��3����ͼ2����D����������һ���㣬���ĺ�����Ϊm���ҩ�3��m����1������D��DK��x���ڵ�K��DK�ֱ��߶�AE��AC�ڵ�G��H���ڵ�D���˶������У�
��DG��GH��HK�������߶��ܷ���ȣ�����ȣ��������D�����ꣻ������ȣ���˵�����ɣ�
���ڢٵ������£��ж�CG��AE��������ϵ����ֱ��д�����ۣ�
���𰸡���1��y����x2��2x+3��y��2x+6��y��x+3����2��ֱ�������Σ�����������3������ȣ�����2��3������AE��2CG
��������
��1���趥��ʽ����A��������룬�ٻ�Ϊһ��ʽ�����ݳ��������3�������a��ֵ���ɴ˿ɵ������߽���ʽ����ֱ��AE��AC�Ľ���ʽ���ٷֱ�A�㡢E����뼴�����ֱ��AE�Ľ���ʽ����A�㡢C����뼴�����ֱ��AC����ʽ��
��2���ֱ����AC2��CE2��AE2�����ù��ɶ������涨�������ж���
��3���������D��G��H�����꣬��ʾDG��HK��GH���ȣ��ȸ���DG��HK�г��������xֵ���پݴ����DG��HK��GH���ȣ����ɵý⣻�ڷֱ����CG��AE�ij��ȣ����ɵó����ǵ�������ϵ��
�⣺��1�������ߵı���ʽΪ��y��a��x+1��2+4��ax2+2ax+a+4��
��a+4��3����ã�a����1��
�������ߵı���ʽΪ��y����x2��2x+3��
��ֱ��AE�Ľ���ʽΪ��![]() ��
��
����A����3��0����E����1��4�����������һ�κ�������ʽ��
![]() ��
��
��ã�![]() ��
��
��ֱ��AE�ı���ʽΪ��y��2x+6��
��ֱ��AC�Ľ���ʽΪ��![]() ��
��
����A����3��0����C��0��3�����������һ�κ�������ʽ��
![]() ��
��
��ã�![]() ��
��
��ֱ��AC�ı���ʽΪ��y��x+3��
��2����A��C��E������ֱ�Ϊ������3��0������0��3��������1��4����
��AC2��![]() =18��CE2��
=18��CE2��![]() =2��AE2��
=2��AE2��![]() =20��
=20��
��AC2+CE2��AE2�����ACEΪֱ�������Σ�
��3�������D��G��H������ֱ�Ϊ����x����x2��2x+3������x��2x+6������x��x+3����
DG����x2��2x+3��2x��6����x2��4x��3��HK��x+3��GH��2x+6��x��3��x+3��
��DG��HKʱ����x2��4x��3��x+3����ã�x����2��3����ȥ��3������x����2��
��x����2ʱ��DG��HK��GH��1��
��DG��GH��HK�������߶����ʱ����D������Ϊ������2��3����
���ɢٵĵ�G������Ϊ������2��2��
CG��![]() ��
��![]() ��AE��
��AE��![]() ��2
��2![]() ��
��
��AE��2CG��


 ��ְٷְټ���ϵ�д�
��ְٷְټ���ϵ�д� �����ƻ���ĩ��̶�100��ϵ�д�
�����ƻ���ĩ��̶�100��ϵ�д� �ܿ���ȫ��100��ϵ�д�
�ܿ���ȫ��100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣��ı���![]() ��֪�Σ�
��֪�Σ�![]() ����
����![]() ���߶�
���߶�![]() ��һ����(����
��һ����(����![]() �غ�)����
�غ�)����![]() ���߶�
���߶�![]() �ӳ�����һ���㣬����
�ӳ�����һ���㣬����![]() ��
��![]() �ڵ�
�ڵ�![]() .��
.��![]() ����֪
����֪![]() ��
��![]() ֮��ĺ�����ϵ��ͼ����ʾ.
֮��ĺ�����ϵ��ͼ����ʾ.
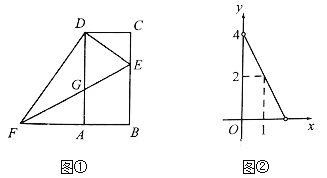
��1����ͼ����![]() ��
��![]() �ĺ�������ʽ;
�ĺ�������ʽ;
��2����֤:![]() ;
;
��3���Ƿ����![]() ��ֵ��ʹ��
��ֵ��ʹ��![]() �ǵ���������?������ڣ����
�ǵ���������?������ڣ����![]() ��ֵ;��������ڣ�˵������
��ֵ;��������ڣ�˵������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���![]() ��
��![]() ��
��![]() ��
��![]() ��������
Ϊ��������![]() ���е�
���е�![]() ��
��![]() �IJ��ֶ�Ӧֵ���±���
�IJ��ֶ�Ӧֵ���±���
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
���½��ۣ�
�ٶ��κ���![]() ����СֵΪ
����СֵΪ![]() ��
��
�ڵ�![]() ʱ��
ʱ��![]() ��
��![]() �����������
�����������
�۶��κ���![]() ��ͼ����
��ͼ����![]() ��ֻ��һ�����㣻
��ֻ��һ�����㣻
�ܵ�![]() ʱ��
ʱ��![]() .
.
������ȷ�Ľ����У� ����
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
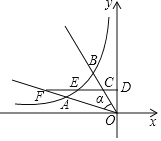
����Ŀ����ͼ��������������˫����y=![]() ��k��0��x��0������A��B���㣬��OB��ȡ��C����CD��y���ڵ�D���ֱ�˫����y=
��k��0��x��0������A��B���㣬��OB��ȡ��C����CD��y���ڵ�D���ֱ�˫����y=![]() ������OA�ڵ�E��F����OA=2AF��OC=2CB����
������OA�ڵ�E��F����OA=2AF��OC=2CB����![]() ��ֵΪ______��
��ֵΪ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ��ֱ������ϵ�У�һ�κ���y����x+b��ͼ���뷴��������y����![]() �ڵڶ������ڵ�ͼ���ཻ�ڵ�A����x��ĸ����ύ�ڵ�B����y��ĸ����ύ�ڵ�C��
�ڵڶ������ڵ�ͼ���ཻ�ڵ�A����x��ĸ����ύ�ڵ�B����y��ĸ����ύ�ڵ�C��
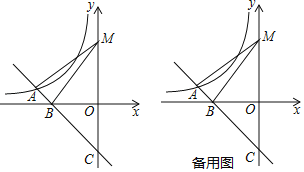
��1�����BCO�Ķ�����
��2����y����һ��M����������4����AM��BM�����A�����ꣻ
��3���ڣ�2���������£�����P��y���ϣ���Q��ƽ��ֱ������ϵ�е�һ�㣬���Ե�A��M��P��QΪ������ı���������ʱ����ֱ��д����Q�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ҵ�����һ���Ʒ��ÿ���ijɱ���50Ԫ��Ϊ�˺������ۣ�Ͷ���г��������������г����飬���۵�����100Ԫʱ��ÿ�����������50���������۵���ÿ����1Ԫ��ÿ��Ϳɶ��۳�5������Ҫ�����۵��۲��õ��ڳɱ���
��1�������۵���Ϊ70Ԫʱ��ÿ������������Ƕ��٣�
��2�����ÿ�����������y��Ԫ�������۵���x��Ԫ��֮��ĺ�����ϵʽ��������Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3���������ҵÿ����ܳɱ�������7000Ԫ����ô���۵���Ϊ����Ԫʱ��ÿ����������������������Ƕ��٣���ÿ����ܳɱ���ÿ���ijɱ���ÿ�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ϣ�С�h��Ҫ������ѧ����ѧ֪ʶ����ij������������ɽ��AE�ĸ߶ȣ�������ɽ���µĵ�E�����ɽ��A��������30����Ȼ���������¶�i=1��1��б�°��ٶ�20��/�ֲ���15���ӵ���C������ʱ����õ�A�ĸ�����15����ͼ�е�A��B��E��D��C��ͬһƽ���ڣ��ҵ�D��E��B��ͬһˮƽֱ���ϣ��������������ɽ��AE�ĸ߶�AB������ȷ��0.1�ף��ο����ݣ�![]() ��1.41����
��1.41����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
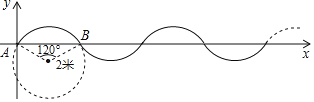
����Ŀ����ͼ���ڵ�λ����Ϊ1��ƽ��ֱ������ϵ�У��������ɰ뾶Ϊ2�ף�Բ�Ľ�Ϊ120��Բ����θ��Ʋ���β���Ӷ��ɣ�����һ��P��A��AΪ����ԭ�㣩����ÿ��![]() ���ٶ������������˶������ڵ�2020��ʱ��P��������Ϊ_____��
���ٶ������������˶������ڵ�2020��ʱ��P��������Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ϸʰٴ����½���40̨�յ�����60̨����䣬�ƻ�����������ļס����������������ۣ�����70̨���������꣬30̨���������꣮�������������������ֵ���ÿ̨������Ԫ�����±���
�յ��� | ����� | |
�������� | 200 | 170 |
�������� | 160 | 150 |
�輯�ŵ������������x̨�յ���������������100̨������������Ϊy��Ԫ����
��1����y����x�ĺ�����ϵʽ�������x��ȡֵ��Χ��
��2��Ϊ�˴��������ž������Լ�������Ŀյ���ÿ̨����aԪ���ۣ��������������䣬����������ÿ̨�յ�����������Ȼ���ڼ����������۵�ÿ̨�����������ʸü���Ӧ�������Ƶ��䷽��������ʹ������ﵽ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com