
【题目】二次函数![]() (
(![]() ,
,![]() ,
,![]() 为常数,且
为常数,且![]() )中的
)中的![]() 与
与![]() 的部分对应值如下表:
的部分对应值如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
以下结论:
①二次函数![]() 有最小值为
有最小值为![]() ;
;
②当![]() 时,
时,![]() 随
随![]() 的增大而增大;
的增大而增大;
③二次函数![]() 的图象与
的图象与![]() 轴只有一个交点;
轴只有一个交点;
④当![]() 时,
时,![]() .
.
其中正确的结论有( )个
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
根据表中数据,可获取相关信息:抛物线的顶点坐标为(1,-4),开口向上,与x轴的两个交点坐标是(-1,0)和(3,0),据此即可得到答案.
①由表格给出的数据可知(0,-3)和(2,-3)是一对对称点,所以抛物线的对称轴为![]() =1,即顶点的横坐标为x=1,所以当x=1时,函数取得最小值-4,故此选项正确;
=1,即顶点的横坐标为x=1,所以当x=1时,函数取得最小值-4,故此选项正确;
②由表格和①可知当x<1时,函数y随x的增大而减少;故此选项错误;
③由表格和①可知顶点坐标为(1,-4),开口向上,∴二次函数![]() 的图象与x轴有两个交点,一个是(-1,0),另一个是(3,0);故此选项错误;
的图象与x轴有两个交点,一个是(-1,0),另一个是(3,0);故此选项错误;
④函数图象在x轴下方y<0,由表格和③可知,二次函数![]() 的图象与x轴的两个交点坐标是(-1,0)和(3,0),∴当
的图象与x轴的两个交点坐标是(-1,0)和(3,0),∴当![]() 时,y<0;故此选项正确;
时,y<0;故此选项正确;
综上:①④两项正确,
故选:B.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
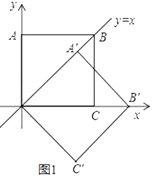
【题目】在平面直角坐标系中,O为原点,边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,现将正方形OABC绕点O顺时针旋转.
(1)如图①,当点A的对应的A′落在直线y=x上时,点A′的对应坐标为________;点B的对应点B′的坐标为_________;
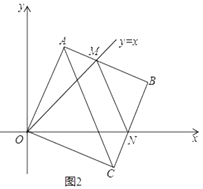
(2)旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N,当A点第一次落在直线y=x上时,停止旋转.
①如图2,在正方形OABC旋转过程中,线段AM,MN,NC三者满足什么样的数量关系?请说明理由;
②当AC∥MN时,求△MBN内切圆的半径(直接写出结果即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
材料1:在处理分数和分式问题时,有时由于分子比分母大,或者分子的次数高于分母的次数,在实际运算时往往难度比较大,这时我们可以将假分数(分式)拆分成一个整数(整式)与一个真分数(式)的和(差)的形式,通过对简单式的分析来解决问题,我们称之为分离整数法.此法在处理分式或整除问题时颇为有效.
例:将分式![]() 拆分成一个整式与一个分式(分子为整数)的和的形式.
拆分成一个整式与一个分式(分子为整数)的和的形式.
解:设x+2=t,则x=t﹣2.
∴原式=![]()
∴![]()
这样,分式![]() 就拆分成一个整式(x﹣5)与一个分式
就拆分成一个整式(x﹣5)与一个分式![]() 的和的形式.
的和的形式.
根据以上阅读材料回答下列问题:
(1)将分式![]() 拆分成一个整式与一个分子为整数的分式的和的形式,则结果为 ;
拆分成一个整式与一个分子为整数的分式的和的形式,则结果为 ;
(2)已知分式![]() 的值为整数,求整数x的值;
的值为整数,求整数x的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在Rt△ABC中,∠BAC=90°,CD为∠ACB的平分线,将∠ACB沿CD所在的直线对折,使点B落在点B′处,连结AB',BB',延长CD交BB'于点E,设∠ABC=2α(0°<α<45°).
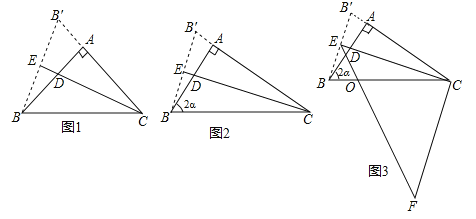
(1)如图1,若AB=AC,求证:CD=2BE;
(2)如图2,若AB≠AC,试求CD与BE的数量关系(用含α的式子表示);
(3)如图3,将(2)中的线段BC绕点C逆时针旋转角(α+45°),得到线段FC,连结EF交BC于点O,设△COE的面积为S1,△COF的面积为S2,求![]() (用含α的式子表示).
(用含α的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年5月的第二个星期日即为母亲节,“父母恩深重,恩怜无歇时”,许多市民喜欢在母亲节为母亲送花,感恩母亲,祝福母亲.今年节日前夕,某花店采购了一批康乃馨,经分析上一年的销售情况,发现这种康乃馨每天的销售量y(支)是销售单价x(元)的一次函数,已知销售单价为7元/支时,销售量为16支;销售单价为8元/支时,销售量为14支.
(1)求这种康乃馨每天的销售量y(支)关于销售单价x(元/支)的一次函数解析式;
(2)若按去年方式销售,已知今年这种康乃馨的进价是每支5元,商家若想每天获得42元的利润,销售单价要定为多少元?
(3)在(2)的条件下,当销售单价x为何值时,花店销售这种康乃馨每天获得的利润最大?并求出获得的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC、BD相交于点O,点E、F分别是边AD、AB上的点,连结OE、OF、EF.若AB=7,BC=5![]() ,∠DAB=45°,则①点C到直线AB的距离是_____.②△OEF周长的最小值是________.
,∠DAB=45°,则①点C到直线AB的距离是_____.②△OEF周长的最小值是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
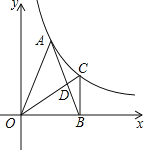
【题目】如图,A为反比例函数y=![]() (其中x>0)图象上的一点,在x轴正半轴上有一点B,OB=4.连接OA、AB,且OA=AB=2
(其中x>0)图象上的一点,在x轴正半轴上有一点B,OB=4.连接OA、AB,且OA=AB=2![]() .
.
(1)求k的值;
(2)过点B作BC⊥OB,交反比例函数y=![]() (x>0)的图象于点C.
(x>0)的图象于点C.
①连接AC,求△ABC的面积;
②在图上连接OC交AB于点D,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线y=ax2+bx+3(a≠0)与x轴分别交于A(﹣3,0),B两点,与y轴交于点C,抛物线的顶点E(﹣1,4),对称轴交x轴于点F.
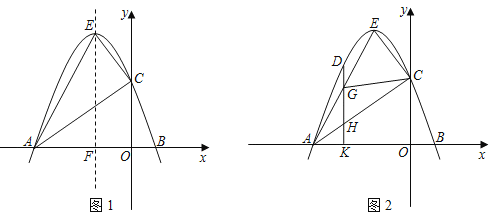
(1)请直接写出这条抛物线和直线AE、直线AC的解析式;
(2)连接AC、AE、CE,判断△ACE的形状,并说明理由;
(3)如图2,点D是抛物线上一动点,它的横坐标为m,且﹣3<m<﹣1,过点D作DK⊥x轴于点K,DK分别交线段AE、AC于点G、H.在点D的运动过程中,
①DG、GH、HK这三条线段能否相等?若相等,请求出点D的坐标;若不相等,请说明理由;
②在①的条件下,判断CG与AE的数量关系,并直接写出结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com