
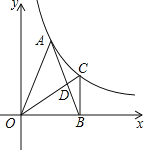
【题目】如图,A为反比例函数y=![]() (其中x>0)图象上的一点,在x轴正半轴上有一点B,OB=4.连接OA、AB,且OA=AB=2
(其中x>0)图象上的一点,在x轴正半轴上有一点B,OB=4.连接OA、AB,且OA=AB=2![]() .
.
(1)求k的值;
(2)过点B作BC⊥OB,交反比例函数y=![]() (x>0)的图象于点C.
(x>0)的图象于点C.
①连接AC,求△ABC的面积;
②在图上连接OC交AB于点D,求![]() 的值.
的值.
【答案】(1)k=12;(2)①3;②![]()
【解析】
(1)过点A作AH⊥x轴,垂足为点H,AH交OC于点M,利用等腰三角形的性质可得出DH的长,利用勾股定理可得出AH的长,进而可得出点A的坐标,再利用反比例函数图象上点的坐标特征即可求出k值;
(2)①由三角形面积公式可求解;
②由OB的长,利用反比例函数图象上点的坐标特征可得出BC的长,利用三角形中位线定理可求出MH的长,进而可得出AM的长,由AM∥BC可得出△ADM∽△BDC,利用相似三角形的性质即可求出![]() 的值.
的值.
(1)过点A作AH⊥x轴,垂足为点H,AH交OC于点M,如图所示.
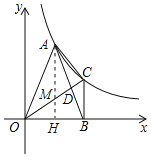
∵OA=AB,AH⊥OB,
∴![]() ,
,
∴![]() ,
,
∴点A的坐标为(2,6).
∵A为反比例函数![]() 图象上的一点,
图象上的一点,
∴![]() ;
;
(2)①∵BC⊥x轴,OB=4,点C在反比例函数![]() 上,
上,
∴![]() ,
,
∵AH⊥OB,
∴AH∥BC,
∴点A到BC的距离=BH=2,
∴S△ABC![]() ;
;
②∵BC⊥x轴,OB=4,点C在反比例函数![]() 上,
上,
∴![]() ,
,
∵AH∥BC,OH=BH,
∴MH=![]() BC=
BC=![]() ,
,
∴![]()
∵AM∥BC,
∴△ADM∽△BDC,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),与x轴交于另一点B,抛物线的顶点为D.
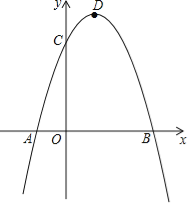
(1)求此二次函数解析式;
(2)连接DC、BC、DB,求证:△BCD是直角三角形;
(3)在对称轴右侧的抛物线上是否存在点P,使得△PDC为等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王某月手机话费中的各项费用统计情况见下列图表,请你根据图表信息完成下列各题:
项目 | 月功能费 | 基本话费 | 长途话费 | 短信费 |
金额/元 | 5 | ▲ | ▲ | 25 |
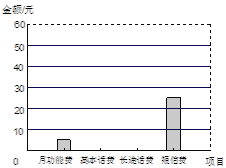
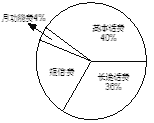
(1)该月小王手机话费共有多少元?
(2)扇形统计图中,表示短信费的扇形的圆心角为多少度?
(3)请将表格补充完整;
(4)请将条形统计图补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() (
(![]() ,
,![]() ,
,![]() 为常数,且
为常数,且![]() )中的
)中的![]() 与
与![]() 的部分对应值如下表:
的部分对应值如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
以下结论:
①二次函数![]() 有最小值为
有最小值为![]() ;
;
②当![]() 时,
时,![]() 随
随![]() 的增大而增大;
的增大而增大;
③二次函数![]() 的图象与
的图象与![]() 轴只有一个交点;
轴只有一个交点;
④当![]() 时,
时,![]() .
.
其中正确的结论有( )个
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示,已知正方形ABCD和正方形AEFG,连接DG,BE.

(1)发现:当正方形AEFG绕点A旋转,如图②所示.
①线段DG与BE之间的数量关系是 ;
②直线DG与直线BE之间的位置关系是 ;
(2)探究:如图③所示,若四边形ABCD与四边形AEFG都为矩形,且AD=2AB,AG=2AE时,上述结论是否成立,并说明理由.
(3)应用:在(2)的情况下,连接BG、DE,若AE=1,AB=2,求BG2+DE2的值(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
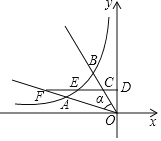
【题目】如图,角α的两边与双曲线y=![]() (k<0,x<0)交于A、B两点,在OB上取点C,作CD⊥y轴于点D,分别交双曲线y=
(k<0,x<0)交于A、B两点,在OB上取点C,作CD⊥y轴于点D,分别交双曲线y=![]() 、射线OA于点E、F,若OA=2AF,OC=2CB,则
、射线OA于点E、F,若OA=2AF,OC=2CB,则![]() 的值为______.
的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,一次函数y=﹣x+b的图象与反比例函数y=﹣![]() 在第二象限内的图象相交于点A,与x轴的负半轴交于点B,与y轴的负半轴交于点C.
在第二象限内的图象相交于点A,与x轴的负半轴交于点B,与y轴的负半轴交于点C.
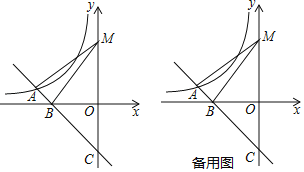
(1)求∠BCO的度数;
(2)若y轴上一点M的纵坐标是4,且AM=BM,求点A的坐标;
(3)在(2)的条件下,若点P在y轴上,点Q是平面直角坐标系中的一点,当以点A、M、P、Q为顶点的四边形是菱形时,请直接写出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,活动课上,小玥想要利用所学的数学知识测量某个建筑地所在山坡AE的高度,她先在山脚下的点E处测得山顶A的仰角是30°,然后,她沿着坡度i=1:1的斜坡按速度20米/分步行15分钟到达C处,此时,测得点A的俯角是15°.图中点A、B、E、D、C在同一平面内,且点D、E、B在同一水平直线上,求出建筑地所在山坡AE的高度AB.(精确到0.1米,参考数据:![]() ≈1.41).
≈1.41).

查看答案和解析>>
科目:初中数学 来源: 题型:
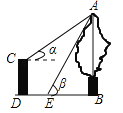
【题目】如图,CD是一高为4米的平台,AB是与CD底部相平的一棵树,在平台顶C点测得树顶A点的仰角α=30°,从平台底部向树的方向水平前进3米到达点E,在点E处测得树顶A点的仰角β=60°,求树高AB(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com