
分析 首先设个位数字为x,则十位数字为(2x+1),则原两位数可表示为10(2x+1)+x,数字对调后所得两位数是[10x+(2x+1)],再根据“将两个数对调后得到的两位数是原两位数减去2后的一半”可得方程:[10x+(2x+1)]=$\frac{1}{2}$[10(2x+1)+x-2],解方程得到个位数,进而可得十位数字.
解答 解:设个位数字为x,则十位数字为(2x+1),
依题意得:[10x+(2x+1)]=$\frac{1}{2}$[10(2x+1)+x-2],
解得x=2,
则2x+1=5,
故这个两位数是52.
答:这个两位数是52.
点评 此题主要考查了一元一次方程的应用,关键是表示出原两位数与新的两位数,根据数之间的关系列出方程.


科目:初中数学 来源: 题型:选择题
| A. | 点A在圆上 | B. | 点A在圆内 | C. | 点A在圆外 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
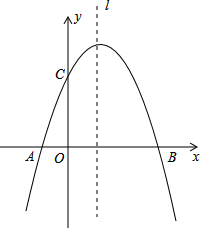 已知:抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴,M为它的顶点
已知:抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴,M为它的顶点查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com