
|
|
|


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:
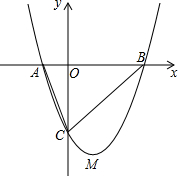 (1)数学小组的单思稿同学认为形如的抛物线y=ax2+bx+c,系数a、b、c一旦确定,抛物线的形状、大小、位置就不会变化,所以称数a、b、c为抛物线y=ax2+bx+c的特征数,记作{a,b,c};请求出与y轴交于点C(0,-3)的抛物线y=x2-2x+k在单同学眼中的特征数;
(1)数学小组的单思稿同学认为形如的抛物线y=ax2+bx+c,系数a、b、c一旦确定,抛物线的形状、大小、位置就不会变化,所以称数a、b、c为抛物线y=ax2+bx+c的特征数,记作{a,b,c};请求出与y轴交于点C(0,-3)的抛物线y=x2-2x+k在单同学眼中的特征数;查看答案和解析>>
科目:初中数学 来源: 题型:
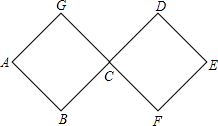 如图,连接在一起的两个正方形的边长都为1cm,一个微型机器人由点A开始按ABCDEFCGA…的顺序沿正方形的边循环移动.当微型机器人移动了2015cm时,它停在
如图,连接在一起的两个正方形的边长都为1cm,一个微型机器人由点A开始按ABCDEFCGA…的顺序沿正方形的边循环移动.当微型机器人移动了2015cm时,它停在查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com