
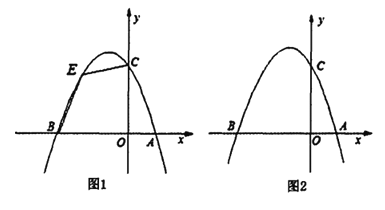
【题目】如图1,已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(l)求抛物线的表达式;
(2)如图l,若点![]() 为第二象限抛物线上一动点,连接
为第二象限抛物线上一动点,连接![]() ,求四边形
,求四边形![]() 面积的最大值,并求此时
面积的最大值,并求此时![]() 点的坐标;
点的坐标;
(3)如图2,在![]() 轴上是否存在一点
轴上是否存在一点![]() 使得
使得![]() 为等腰三角形?若存在,请求出所有符合条件的点
为等腰三角形?若存在,请求出所有符合条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 最大值为
最大值为![]() ,点
,点![]() 坐标为
坐标为![]() ;(3)存在符合条件的点
;(3)存在符合条件的点![]() ,其坐标为
,其坐标为![]() 或
或![]() ,或
,或![]() 或
或![]()
【解析】
(1)将点A、B的坐标代入解析式即可得到答案;
(2)设![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,利用
,利用![]() 求出解析式即得到面积的最大值及点E的坐标;
求出解析式即得到面积的最大值及点E的坐标;
(3)存在,分以点C、A为顶点及线段AC为底边三种情况,分别求出点D的坐标即可.
解:(1)由题知:
![]() ,解得:
,解得:![]()
∴所求抛物线表达式为![]()
(2)过点![]() 作
作![]() 轴于点
轴于点![]()
设![]()
∴![]() ,
,![]() ,
,![]() ,
,
∴![]()
![]()
![]()
![]()
∴当![]() 时,
时,![]() 最大,且最大值为
最大,且最大值为![]() .
.
当![]() 时,
时,![]()
此时,点![]() 坐标为
坐标为![]()
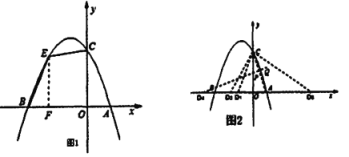
(3)连接![]()
①当点![]() 为顶点,
为顶点,![]() 时,此时
时,此时![]() 为底边的垂直平分线,
为底边的垂直平分线,
满足条件的点![]() ,与点
,与点![]() 关于
关于![]() 轴对称,
轴对称,
∴点![]() 坐标为
坐标为![]()
②当点![]() 为顶点,
为顶点,![]() 时,在
时,在![]() 中,
中,
∵![]() ,
,![]() ,由勾股定理得:
,由勾股定理得:![]() ,
,
以点![]() 为圆心,
为圆心,![]() 的长为半径作弧,交
的长为半径作弧,交![]() 轴于两点
轴于两点![]() ,即为满足条件的点,
,即为满足条件的点,
此时它们的坐标分别为![]() ,
,![]()
③当![]() 为底边时,线段
为底边时,线段![]() 的垂直平分线与
的垂直平分线与![]() 轴的交点
轴的交点![]() ,即为满足条件的点,
,即为满足条件的点,
设垂直![]() 的垂直平分线交
的垂直平分线交![]() 轴于点
轴于点![]() ,过
,过![]() 中点
中点![]() ,
,
∵![]() ,
,![]()
∴![]()
∴![]()
∴![]() ,
,![]() ,
,![]()
![]() ,
, ,
,![]() ,
,
点![]() 的坐标为
的坐标为![]()
综上所述存在符合条件的点![]() ,其坐标为
,其坐标为![]() 或
或![]() ,或
,或![]() 或
或![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
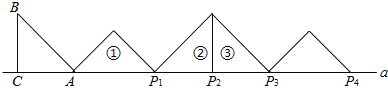
【题目】如图,等腰![]() 中,
中,![]() ,
,![]() ,且AC边在直线a上,将
,且AC边在直线a上,将![]() 绕点A顺时针旋转到位置①可得到点
绕点A顺时针旋转到位置①可得到点![]() ,此时
,此时![]() ;将位置①的三角形绕点
;将位置①的三角形绕点![]() 顺时针旋转到位置②,可得到点
顺时针旋转到位置②,可得到点![]() ,此时
,此时![]() ;将位置②的三角形绕点
;将位置②的三角形绕点![]() 顺时针旋转到位置③,可得到点
顺时针旋转到位置③,可得到点![]() ,此时
,此时 ![]() ________,…,按此规律继续旋转,直至得到点
________,…,按此规律继续旋转,直至得到点![]() 为止,则
为止,则![]() ________.
________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若凸四边形的两条对角线所夹锐角为60°,我们称这样的凸四边形为“完美四边形”.
(1)①在“平行四边形、梯形、菱形、正方形”中,一定不是“完美四边形”的有 ;
②若矩形ABCD是“完美四边形”,且AB=4,则BC= ;
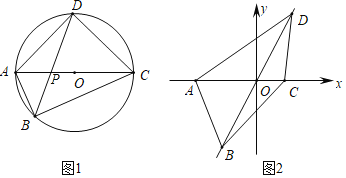
(2)如图1,“完美四边形”ABCD内接于⊙O,AC与BD相交于点P,且对角线AC为直径,AP=1,PC=5,求另一条对角线BD的长;
(3)如图2,平面直角坐标系中,已知“完美四边形”ABCD的四个顶点A(﹣3,0)、C (2,0),B在第三象限,D在第一象限,AC与BD交于点O,直线BD的斜率为![]() ,且四边形ABCD的面积为15
,且四边形ABCD的面积为15![]() ,若二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)的图象同时经过这四个顶点,求a的值.
,若二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)的图象同时经过这四个顶点,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:(保留作图痕迹,不写做法)
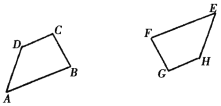
(1)已知:如图,四边形ABCD与四边形EFGH成中心对称,试画出它们的对称中心O。
(2)考古学家在考古过程中发现一个圆盘,但是因为历史悠久,已经有一部分缺失,如图所示.现希望复原圆盘,需要先找到圆盘的圆心,才能继续完成后续修复工作.请利用直尺(无刻度)和圆规,在图中找出圆心O.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,图形G上点P(x,y)的纵坐标y与其横坐标x的差y-x称为P点的“坐标差”,而图形G上所有点的“坐标差”中的最大值称为图形G的“特征值”
(1)①点A(1,3) 的“坐标差”为 。
②抛物线y=-x2+3x+3的“特征值”为 。
(2)某二次函数y=-x2+bx+c(c≠0) 的“特征值”为1,点B(m,0)与点C分别是此二次函数的图象与x轴和y轴的交点,且点B与点C的“坐标差”相等。
①直接写出m= (用含c的式子表示)
②求此二次函数的表达式。
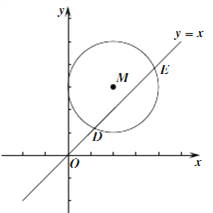
(3)如图,在平面直角坐标系xOy中,以M(2,3)为圆心,2为半径的圆与直线y=x相交于点D、E请直接写出⊙M的“特征值”为 。
查看答案和解析>>
科目:初中数学 来源: 题型:
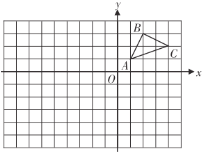
【题目】如图,在边长为1个单位长度的小正方形网格中,![]() 的顶点均在格点上,在建立平面直角坐标系后,点
的顶点均在格点上,在建立平面直角坐标系后,点![]() 的坐标为
的坐标为![]() .
.
(1)将![]() 向左平移3个单位得到
向左平移3个单位得到![]() ,画出
,画出![]() ;
;
(2)在第三象限内,以![]() 为位似中心,将
为位似中心,将![]() 放大到原大的2倍,画出放大后对应的
放大到原大的2倍,画出放大后对应的![]() ;
;
(3)写出![]() 的坐标______,
的坐标______,![]() 的坐标______.
的坐标______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读探索:“任意给定一个矩形A,是否存在另一个矩形B,它的周长和面积分别是已知矩形周长和面积的一半?”(完成下列空格)
(1)当已知矩形A的边长分别为6和1时,小亮同学是这样研究的:
设所求矩形的两边分别是x和y,由题意得方程组: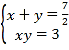 ,消去y化简得:2x2﹣7x+6=0,
,消去y化简得:2x2﹣7x+6=0,
∵△=49﹣48>0,
∴x1=_____,x2=_______,
∴满足要求的矩形B存在.
(2)如果已知矩形A的边长分别为2和1,请你仿照小亮的方法研究是否存在满足要求的矩形B.
(3)如果矩形A的边长为m和n,请你研究满足什么条件时,矩形B存在?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中装有大小和形状相同的3个红球和2个白球,把它们充分搅匀.
(1)“从中任意抽取1个球不是红球就是白球”是 事件,“从中任意抽取1个球是黑球”是 事件;
(2)从中任意抽取1个球恰好是红球的概率是 ;
(3)学校决定在甲、乙两名同学中选取一名作为学生代表发言,制定如下规则:从盒子中任取两个球,若两球同色,则选甲;若两球异色,则选乙.甲、乙两名同学被选中的概率各是多少?你认为这个规则公平吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司销售一种新型产品,现准备从国内和国外两种销售方案中选择一种进行销售.若只在国内销售,销售价格y(元/件)与月销量x(件)的函数关系式为y=-![]() x+150,成本为50元/件,无论销售多少,每月还需支出广告费90000元,设月利润为w内(元),若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10
x+150,成本为50元/件,无论销售多少,每月还需支出广告费90000元,设月利润为w内(元),若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10![]() a
a![]() 40),当月销量为x(件)时,每月还需缴纳
40),当月销量为x(件)时,每月还需缴纳![]() x2元的附加费,设月利润为w外(元).
x2元的附加费,设月利润为w外(元).
(1)当x=1000时,y= 元/件,w内= 元;
(2)分别求出w内,w外与x间的函数关系式(不必写x的取值范围);
(3)当x为何值时,在国内销售的月利润最大?若在国外销售月利润的最大值与在国内销售月利润的最大值相同,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com