
����Ŀ�����壺��ƽ��ֱ������ϵ�У�ͼ��G�ϵ�P(x,y)��������y���������x�IJ�y��x��ΪP��ġ���������ͼ��G�����е�ġ������е����ֵ��Ϊͼ��G�ġ�����ֵ��
(1)�ٵ�A(1,3) �ġ�����Ϊ ��
��������y=��x2+3x+3�ġ�����ֵ��Ϊ ��
(2)ij���κ���y=��x2+bx+c(c��0) �ġ�����ֵ��Ϊ1����B(m,0)���C�ֱ��Ǵ˶��κ�����ͼ����x���y��Ľ��㣬�ҵ�B���C�ġ�������ȡ�
��ֱ��д��m= (�ú�c��ʽ�ӱ�ʾ)
����˶��κ����ı���ʽ��
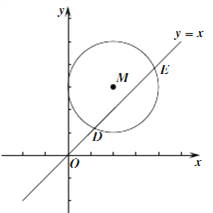
(3)��ͼ����ƽ��ֱ������ϵxOy�У���M(2,3)ΪԲ�ģ�2Ϊ�뾶��Բ��ֱ��y=x�ཻ�ڵ�D��E��ֱ��д����M�ġ�����ֵ��Ϊ ��
���𰸡���1���� 2�� �� 4�� ��2���� m= ��c ; ��
![]() ����3��
����3��![]()
�����������������
��1���������������������Ķ��弴�ɵõ���A��1��3��������
���������Ķ���ɵ������κ���y=��x2+3x+3ͼ���ϵ�������Ϊ�� ![]() �����˹�ϵʽ�䷽�������y-x�����ֵ���Ӷ��õ�������y=��x2+3x+3�ġ�����ֵ����
�����˹�ϵʽ�䷽�������y-x�����ֵ���Ӷ��õ�������y=��x2+3x+3�ġ�����ֵ����
��2����������ɵ���0-m=c-0���ɴ˿ɵ���m=-c��
����m=-c�ɵõ�B������Ϊ��-c��0�����ѵ�B���������![]() �пɵ�
�пɵ�![]() ����
����![]() �ɵ�
�ɵ�![]() ����
����![]() ������
������![]() ������ֵΪ1�ɵã�
������ֵΪ1�ɵã� ![]() �������ɽ��b��c��ֵ���ɴ˼��ɵõ����κ����Ľ���ʽ��
�������ɽ��b��c��ֵ���ɴ˼��ɵõ����κ����Ľ���ʽ��
��3����ͼ������M��ֱ��PF��DE������M�ڵ�P��F������֪������ֱ��PF�Ľ���ʽΪy=-x+5����ֱ��y=x�ϵ����е�������Ϊ0��������ƽ������ֱ��y=x���Ҳ����ֱ��y=xԽԶ�ĵ�������Խ���֪����M�Ͼ���ֱ��y=x��Զ�ĵ��ǵ�P�����P������Ϊ��x��y���ɵ�P��M�ľ���Ϊ2���ɵõ�����x��y�ķ��̣���y=-x+5��ϼ��ɽ�õ�P�����꣬�����Ϳɵõ���M������ֵ��.
���������
��1���� ����A��������1��3����
����A���������3-1= 2��
�� �߶��κ����Ľ���ʽΪ��y=��x2+3x+3��
���ö��κ���ͼ�������е������������ ![]() ��
��
��![]() �����ö��κ���ͼ���ϵ�����������ֵΪ4��
�����ö��κ���ͼ���ϵ�����������ֵΪ4��
��ö��κ���ͼ�������ֵΪ��4��
��2���� ����֪�õ�C������Ϊ��0��c������B������Ϊ��m��0����
���C���������c-0����B���������0-m��
�֡ߵ�B���C�ġ�������ȣ�
��c-0=0-m��
��m=��c��
�� ��m=��c��
��B����c��0����
�������![]() ��
�У�
�ã� ![]() ��
��
��c��0��
��![]() ��
��
��![]() �� ��
�� ��
��![]() �ġ�����Ϊ��
�ġ�����Ϊ��
![]() ��
��
�ߡ�����ֵ��Ϊ1��
��![]() ����
����
���ٴ�����У��ã� ![]()
��![]() ��
��
�������ߵı���ʽΪ![]() ��
��
��3����ͼ������M��ֱ��PF��DE������M�ڵ�P��F��
��ֱ��DE�Ľ���ʽΪ��y=x����M������Ϊ��2��3����
��ֱ��PF�Ľ���ʽΪy=-x+5��
��ֱ��y=x�����е����������0������ֱ��y=x���Ҳ����ֱ��y=xԽԶ�ĵ��������Խ��������M�ϵ�P����ֱ��y=x��Զ��
����P������������M�ġ�����ֵ����
���P��������x��y����
����P����M��2��3���ľ���Ϊ2��
����![]() ��
��
������P��x��y����ֱ��y=-x+5����
��![]() �������
������� ![]() ��
��
����Ӧ���� ![]() ��
��
����P������Ϊ![]() ��
��
����P��������� ![]() ��
��
���M�ġ�����ֵ��Ϊ�� ![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��O��ֱ��Ϊ10����A����B����C�ڡ�O�ϣ���CAB��ƽ���߽���O�ڵ�D��
��1����ͼ�٣���BCΪ��O��ֱ����AB=6����AC��BD��CD�ij���
��2����ͼ�ڣ�����CAB=60�㣬��BD�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
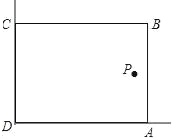
����Ŀ��������У�Ļ�У�ij��ȤС���������ͼ��ʾ��ֱ��ǽ�ǣ������㹻��������28m�������Χ��һ�����λ�ABCD�����ֻΧAB��BC���ߣ�����AB=xm������P����һ������ǽCD��AD�ľ���ֱ���15m��6m��Ҫ�������Χ�ڻ��ڣ����߽磬���������Ĵ�ϸ���������S�����ֵΪ_____m2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
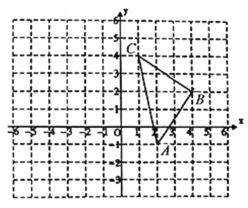
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�![]() ��
��![]() ��
��![]() ��
��
��1���뻭��![]() ����
����![]() ��ԳƵ�
��ԳƵ�![]() ��
��
��2��ֱ��д��![]() �����Ϊ ��
�����Ϊ ��
��3��������̶ȵ�ֱ����![]() ��ƽ����
��ƽ����![]() ��������ͼ�ۼ���
��������ͼ�ۼ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ˮ�����г��������ң����š�����ô�ȹ�˾�����������ӣ�ij��˾������Ƹ�����Ͳ�Ա�����巽�����£�ÿ�²�����750����ÿ������4Ԫ������750���IJ���ÿ������mԪ��
��1����ij������С����ij������500���������� ��Ԫ��
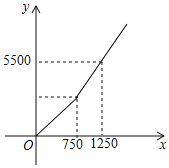
��2����������С����ÿ������Ϊy��Ԫ����ÿ���͵���Ϊx����y��x֮��Ĺ�ϵ��ͼ��ʾ����y��x֮��ĺ�����ϵʽ��
��3����������С����������ij�����ڹ��͵�1200�����Ҽ��͵����������͵�����������5000Ԫ���ʣ��ס����͵������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ƕ��κ���y=ax2+bx+c��a��b��c�dz�����a��0��ͼ���һ���֣���x��Ľ���A�ڵ㣨2��0���ͣ�3��0��֮�䣬�Գ�����x=1����������˵������ab��0����2a+b=0����3a+c��0����a+b��m��am+b����mΪʵ������������1��x��3ʱ��y��0��������ȷ���ǣ�������

A. �٢ڢ� B. �٢ڢ� C. �ڢۢ� D. �ۢܢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
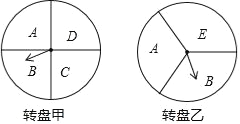
����Ŀ��ij�����ڶ�����ڼ俪չ�Żݻ���������߿���ͨ��ת��ת�̵ķ�ʽ�����ۿ��Żݣ����λ�������ַ�ʽ����ʽһ��ת��ת�̼ף�ָ��ָ�� A����ʱ����������Ʒ����9���Żݡ�ָ��ָ�������������Żݣ���ʽ���� ͬʱת��ת�̼�ת���ң�������ת�̵�ָ��ָ��ÿ���������ĸ��ͬ����������Ʒ����8���Żݣ�����������Żݣ���ÿ��ת���У�ָ��ָ��ÿ�����ǵĿ�������ͬ����ָ��ָ��ֽ��ߣ�������ת��ת�̣�
(1)���˿�ѡ��ʽһ�������� 9 ���Żݵĸ���Ϊ_______��
(2)���˿�ѡ��ʽ����������״ͼ���б����г����п��ܣ�����˿�����8���Żݵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
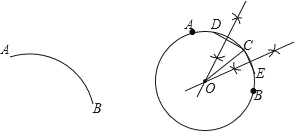
����Ŀ�������ǡ�������AB���ڵ�Բ���ij߹���ͼ���̣�
��֪����AB��
��������AB���ڵ�Բ��
��������ͼ��
��1���ڻ�AB����ȡ������D��C��E��
��2������DC��EC��
��3���ֱ���DC��EC�Ĵ�ֱƽ���ߣ�����ֱƽ���ߵĽ���Ϊ��O��
��4���� OΪԲ�ģ�OC��Ϊ�뾶��Բ��������O��Ϊ�������Ļ�AB���ڵ�Բ��
��ش𣺸ó߹���ͼ��������_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������з��̣�
��1��x��x��1��=1��x
��2��x2+2x��35=0
��3��4x2��3=12x
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com