
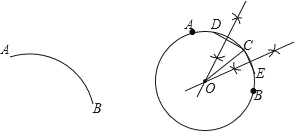
【题目】下面是“作出弧AB所在的圆”的尺规作图过程.
已知:弧AB.
求作:弧AB所在的圆.
作法:如图,
(1)在弧AB上任取三个点D,C,E;
(2)连接DC,EC;
(3)分别作DC和EC的垂直平分线,两垂直平分线的交点为点O.
(4)以 O为圆心,OC长为半径作圆,所以⊙O即为所求作的弧AB所在的圆.
请回答:该尺规作图的依据是_____.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某社区准备在甲乙两位射箭爱好者中选出一人参加集训,两人各射了5箭,小宇根据他们的成绩(单位:环)绘制了如下尚不完整的统计表:
第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
甲成绩 | 9 | 4 | 7 | a | 6 |
乙成绩 | 7 | 5 | 7 | 4 | 7 |
(1)若甲成绩的平均数为6环,求a的值;
(2)若甲成绩的方差为3.6,请计算乙成绩的方差并说明谁的成绩更稳定?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,图形G上点P(x,y)的纵坐标y与其横坐标x的差y-x称为P点的“坐标差”,而图形G上所有点的“坐标差”中的最大值称为图形G的“特征值”
(1)①点A(1,3) 的“坐标差”为 。
②抛物线y=-x2+3x+3的“特征值”为 。
(2)某二次函数y=-x2+bx+c(c≠0) 的“特征值”为1,点B(m,0)与点C分别是此二次函数的图象与x轴和y轴的交点,且点B与点C的“坐标差”相等。
①直接写出m= (用含c的式子表示)
②求此二次函数的表达式。
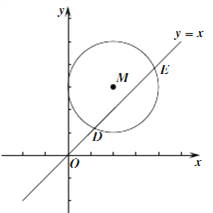
(3)如图,在平面直角坐标系xOy中,以M(2,3)为圆心,2为半径的圆与直线y=x相交于点D、E请直接写出⊙M的“特征值”为 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接我市创建全国文明城市活动,环卫处投资20万元购买并投放一批![]() 型“垃圾清扫车”,因为清扫车需求量增加,计划继续投放
型“垃圾清扫车”,因为清扫车需求量增加,计划继续投放![]() 型清扫车,
型清扫车,![]() 型清扫车的投放数量与
型清扫车的投放数量与![]() 型清扫车的投放数量相同,投资总费用减少
型清扫车的投放数量相同,投资总费用减少![]() ,购买
,购买![]() 型清扫车的单价比购买
型清扫车的单价比购买![]() 型清扫车的单价少50元,则
型清扫车的单价少50元,则![]() 型清扫车每辆车的价格是多少元?设
型清扫车每辆车的价格是多少元?设![]() 型清扫车每辆车的价格为
型清扫车每辆车的价格为![]() 元,根据题意,列方程正确的是( )
元,根据题意,列方程正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() ,二次函数
,二次函数![]() (其中m>4).
(其中m>4).
(1)求二次函数图象的顶点坐标(用含m的代数式表示);
(2)利用函数图象解决下列问题:
①若![]() ,求当
,求当![]() 且
且![]() ≤0时,自变量
≤0时,自变量![]() 的取值范围;
的取值范围;
②如果满足![]() 且
且![]() ≤0时自变量
≤0时自变量![]() 的取值范围内有且只有一个整数,直接写出
的取值范围内有且只有一个整数,直接写出![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC和△A1B1C1中,下列命题中真命题的个数为( )
(1)若∠A=∠A1,∠C=∠C1,则△ABC∽△A1B1C1;
(2)若AC∶A1C1=CB∶C1B1,∠C=∠C1,则△ABC∽△A1B1C1;
(3)若AB=kA1B1,AC=kA1C1(k≠0),∠A=∠A1,则△ABC∽△A1B1C1;
(4)若S△ABC=![]() ,则△ABC∽△A1B1C1.
,则△ABC∽△A1B1C1.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD与四边形A′B′C′D′是位似图形,且它们的对应边的比为3:4,则四边形ABCD与四边形A′B′C′D′的周长之比为______,面积之比为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
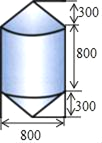
【题目】如图,锚标浮筒是打捞作业中用来标记锚或沉船位置的,它的上下两部分是圆柱,中间是一个圆柱(如图,单位:mm).电镀时,如果每平方米用锌0.11kg,要电镀1000个这样的锚标浮筒需要用多少锌?(精确到1kg)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0)和点B,与y轴交于点C,点C关于抛物线对称轴的对称点为点D,抛物线顶点为H(1,2).
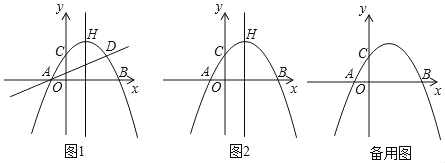
(1)求抛物线的解析式;
(2)点P为直线AD上方抛物线的对称轴上一动点,连接PA,PD.当S△PAD=3,若在x轴上存在一动点Q,使PQ+![]() QB最小,求此时点Q的坐标及PQ+
QB最小,求此时点Q的坐标及PQ+![]() QB的最小值;
QB的最小值;
(3)若点E为抛物线上的动点,点G,F为平面内的点,以BE为边构造以B,E,F,G为顶点的正方形,当顶点F或者G恰好落在y轴上时,求点E的横坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com