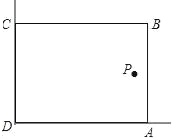
【题目】在美化校园的活动中，某兴趣小组想借助如图所示的直角墙角（两边足够长），用28m长的篱笆围成一个矩形花园ABCD（篱笆只围AB，BC两边），设AB=xm．若在P处有一棵树与墙CD，AD的距离分别是15m和6m，要将这棵树围在花园内（含边界，不考虑树的粗细），则花园面积S的最大值为_____m2．
星级口算天天练系列答案科目：初中数学 来源： 题型：
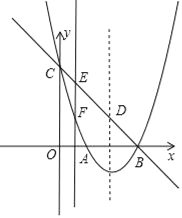
【题目】如图，抛物线y=ax2+bx+c（a≠0）的顶点坐标为（2，﹣1），图象与y轴交于点C（0，3），与x轴交于A、B两点．
（1）求抛物线的解析式；
（2）设抛物线对称轴与直线BC交于点D，连接AC、AD，求△ACD的面积；
（3）点E为直线BC上的任意一点，过点E作x轴的垂线与抛物线交于点F，问是否存在点E使△DEF为直角三角形？若存在，求出点E坐标，若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
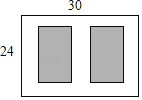
【题目】如图，某小区有一块长为30 m，宽为24 m的矩形空地，计划在其中修建两块相同的矩形绿地，它们的面积之和为480 m2，两块绿地之间及周边有宽度相等的人行通道，则人行通道的宽度为________m．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某社区准备在甲乙两位射箭爱好者中选出一人参加集训，两人各射了5箭，小宇根据他们的成绩（单位：环）绘制了如下尚不完整的统计表：
第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
甲成绩 | 9 | 4 | 7 | a | 6 |
乙成绩 | 7 | 5 | 7 | 4 | 7 |
（1）若甲成绩的平均数为6环，求a的值；
（2）若甲成绩的方差为3.6，请计算乙成绩的方差并说明谁的成绩更稳定?
查看答案和解析>>
科目：初中数学 来源： 题型：
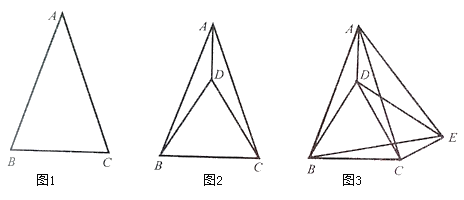
【题目】如图1，张老师在黑板上画出了一个
，其中
，让同学们进行探究．
（1）探究一：
如图2，小明以
为边在内部作等边
，连接
，请直接写出
的度数_____________；
（2）探究二：
如图3，小彬在（1）的条件下，又以
为边作等边
，连接
.判断与的数量关系；并说明理由；
（3）探究三：
如图3，小聪在（2）的条件下，连接
，若
，求
的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义：在平面直角坐标系中，图形G上点P(x,y)的纵坐标y与其横坐标x的差y－x称为P点的“坐标差”，而图形G上所有点的“坐标差”中的最大值称为图形G的“特征值”
(1)①点A(1,3) 的“坐标差”为 。
②抛物线y=－x2+3x+3的“特征值”为 。
(2)某二次函数y=－x2+bx+c(c≠0) 的“特征值”为1，点B(m,0)与点C分别是此二次函数的图象与x轴和y轴的交点，且点B与点C的“坐标差”相等。
①直接写出m= (用含c的式子表示)
②求此二次函数的表达式。
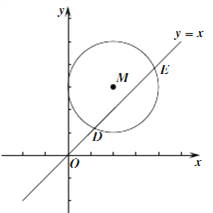
(3)如图，在平面直角坐标系xOy中，以M(2,3)为圆心，2为半径的圆与直线y=x相交于点D、E请直接写出⊙M的“特征值”为 。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知四边形ABCD与四边形A′B′C′D′是位似图形，且它们的对应边的比为3:4，则四边形ABCD与四边形A′B′C′D′的周长之比为______，面积之比为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
