
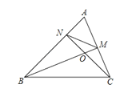
【题目】如图,![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,![]() 交于点
交于点![]() ,连接
,连接![]() .下列结论:①
.下列结论:①![]() ;②图中共有8对相似三角形;③
;②图中共有8对相似三角形;③![]() .其中正确的是______
.其中正确的是______
 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
【题目】某商场以每件280元的价格购进一批商品,当每件商品售价为360元时,每月可售出60件,为了扩大销售,商场决定采取适当降价的方式促销,经调查发现,如果每件商品降价1元,那么商场每月就可以多售出5件.
(1)设商场每件商品降价x元,利润为y元,写出y与x的函数关系式。
(2)当该商品的销售价为多少元时,所获利润最大?最大利润是多少?
(3)要使商场每月销售这种商品的利润达到7200元,且更有利于减少库存,则每件商品应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
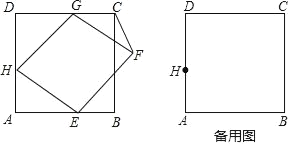
【题目】如图,已知正方形ABCD的边长为3,菱形EFGH的三个顶点E、G、H分别在正方形的边AB、CD、DA上,AH=1,联结CF.
(1)当DG=1时,求证:菱形EFGH为正方形;
(2)设DG=x,△FCG的面积为y,写出y关于x的函数解析式,并指出x的取值范围;
(3)当DG=![]() 时,求∠GHE的度数.
时,求∠GHE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“一带一路”战略的影响下,某茶叶经销商准备把“茶路”融入“丝路”,经计算,他销售10斤A级别和20斤B级别茶叶的利润为4000元,销售20斤A级别和10斤B级别茶叶的利润为3500元
(1)分别求出每斤A级别茶叶和每斤B级别茶叶的销售利润;
(2)若该经销商一次购进两种级别的茶叶共200斤用于出口.设购买A级别茶叶a斤(70≤a≤120),销售完A、B两种级别茶叶后获利w元.
①求出w与a之间的函数关系式;
②该经销商购进A、B两种级别茶叶各多少斤时,才能获取最大的利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
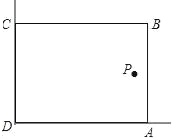
【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),则花园面积S的最大值为_____m2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“作圆的内接正方形”的尺规作图过程。
已知:⊙O.
求作:圆的内接正方形.
如图,
(1)过圆心O作直线AC,与⊙O相交于A,C两点;
(2)过点O作直线BD⊥AC,交⊙O于B,D两点;
(3)连接AB,BC,CD,DA。
∴四边形ABCD为所求。

请回答:该尺规作图的依据是____________________________。(写出两条)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】涟水外卖市场竞争激烈,美团、饿了么等公司订单大量增加,某公司负责招聘外卖送餐员,具体方案如下:每月不超出750单,每单收入4元;超出750单的部分每单收入m元.
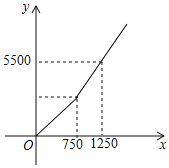
(1)若某“外卖小哥”某月送了500单,收入 元;
(2)若“外卖小哥”每月收入为y(元),每月送单量为x单,y与x之间的关系如图所示,求y与x之间的函数关系式;
(3)若“外卖小哥”甲和乙在某个月内共送单1200单,且甲送单量低于乙送单量,共收入5000元,问:甲、乙送单量各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
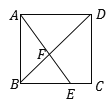
【题目】如图所示,在正方形ABCD中,点E是BC边上一点,且BE:EC=2:1,AE与BD交于点F,则△AFD与四边形DFEC的面积之比是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com