
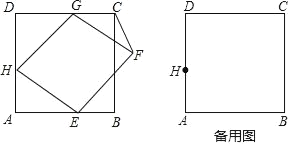
【题目】如图,已知正方形ABCD的边长为3,菱形EFGH的三个顶点E、G、H分别在正方形的边AB、CD、DA上,AH=1,联结CF.
(1)当DG=1时,求证:菱形EFGH为正方形;
(2)设DG=x,△FCG的面积为y,写出y关于x的函数解析式,并指出x的取值范围;
(3)当DG=![]() 时,求∠GHE的度数.
时,求∠GHE的度数.
【答案】(1)详见解析;(2)![]() (3)60°
(3)60°
【解析】
(1)先求出HG,再判断出△AHE≌△DGH,得出∠AHE=∠DGH,进而判断出∠GHE=90,即可得出结论;
(2)先判断出∠HEA=∠FGM,进而判断出△AHE≌△MFG.得出FM=HA=1,即可得出结论;
(3)利用勾股定理依次求出GH=![]() ,AE=
,AE=![]() ,GE=
,GE=![]() ,进而判断出GH=HE=GE,即可得出结论
,进而判断出GH=HE=GE,即可得出结论
解:(1)在正方形ABCD中,
∵AH=1,
∴DH=2.
又∵DG=1,
∴HG=![]()
在△AHE和△DGH中,
∵∠A=∠D=90°,AH=DG=1,EH=HG=![]() ,
,
∴△AHE≌△DGH,
∴∠AHE=∠DGH.
∵∠DGH+∠DHG=90°,∠AHE+∠DHG=90°.
∴∠GHE=90°
所以菱形EFGH是正方形;
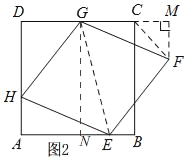
(2)如图1,过点F作FM⊥DC交DC所在直线于M,联结GE.
∵AB∥CD,
∴∠AEG=∠MGE.
∵HE∥GF,
∴∠HEG=∠FGE.
∴∠HEA=∠FGM,
在△AHE和△MFG中,
∵∠A=∠M=90°,EH=GF.
∴△AHE≌△MFG.
∴FM=HA=1.
即无论菱形EFGH如何变化,点F到直线CD的距离始终为定值1,
∴y=![]() GCFM=
GCFM=![]() (3﹣x)×1=﹣
(3﹣x)×1=﹣![]() x+
x+![]() (0≤x≤
(0≤x≤![]() );
);
(3)如图2,当DG=![]() 时,
时,
在Rt△HDG中,DH=2,根据勾股定理得,GH=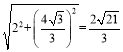 ;
;
∴HE=GH=![]() ,
,
在Rt△AEH中,根据勾股定理得,AE= ,
,
过点G作GN⊥AB于N,
∴EN=AE﹣DG=![]()
在Rt△ENG中,根据勾股定理得,GE=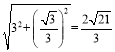
∴GH=HE=GE,
∴△GHE为等边三角形.
∴∠GHE=60°.



科目:初中数学 来源: 题型:
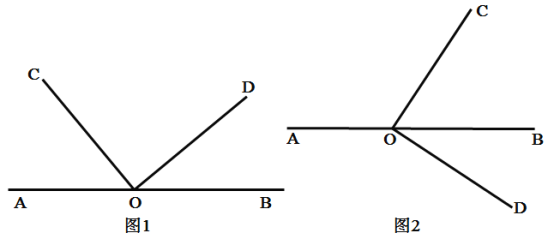
【题目】如图,点O是直线AB上的一点,OD⊥OC,过点O作射线OE平分∠BOC.
(1)如图1,如果∠AOC=50°,依题意补全图形,写出求∠DOE度数的思路(不需要写出完整的推理过程);
(2)当OD绕点O顺时针旋转一定的角度得到图2,使得直角边OC在直线AB的上方,若∠AOC=α,其他条件不变,依题意补全图形,并求∠DOE的度数(用含α的代数式表示);
(3)当OD绕点O继续顺时针旋转一周,回到图1的位置,在旋转过程中你发现∠AOC与∠DOE(0°≤∠AOC≤180°,0°≤∠DOE≤180°)之间有怎样的数量关系?请直接写出你的发现.
查看答案和解析>>
科目:初中数学 来源: 题型:
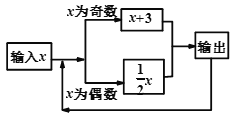
【题目】如图,是某一计算程序,回答如下问题:
(1)当输入某数后,第一次得到的结果为5,则输入的数值x=_______;
(2)若输入的x的值为16时,第1次得到的结果为8,第2次得到的结果为4,…,则第2019次得到的结果是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了改善教室空气环境,某校九年级1班班委会计划到朝阳花卉基地购买绿植.已知该基地一盆绿萝与一盆吊兰的价格之和是12元.班委会决定用60元购买绿萝,用90元购买吊兰,所购绿萝数量正好是吊兰数量的两倍.
(1)分别求出每盆绿萝和每盆吊兰的价格;
(2)该校九年级所有班级准备一起到该基地购买绿萝和吊兰共计90盆,其中绿萝数量不超过吊兰数量的一半,该基地特地对吊兰价格给出了如下的优惠政策,一次性购买的吊兰超过20盆时,超过部分的吊兰每盆的价格打8折,根据该基地的优惠信息,九年级购买这两种绿植各多少盆时总费用最少?最少费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
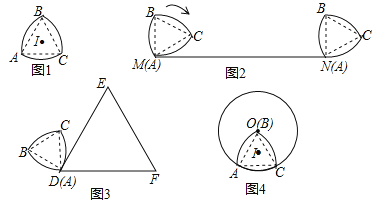
【题目】如图1,等边△ABC的边长为3,分别以顶点B、A、C为圆心,BA长为半径作![]() 、
、![]() 、
、![]() ,我们把这三条弧所组成的图形称作莱洛三角形,显然莱洛三角形仍然是轴对称图形,设点l为对称轴的交点.
,我们把这三条弧所组成的图形称作莱洛三角形,显然莱洛三角形仍然是轴对称图形,设点l为对称轴的交点.
(1)如图2,将这个图形的顶点A与线段MN作无滑动的滚动,当它滚动一周后点A与端点N重合,则线段MN的长为 ;
(2)如图3,将这个图形的顶点A与等边△DEF的顶点D重合,且AB⊥DE,DE=2π,将它沿等边△DEF的边作无滑动的滚动当它第一次回到起始位置时,求这个图形在运动过程中所扫过的区域的面积;
(3)如图4,将这个图形的顶点B与⊙O的圆心O重合,⊙O的半径为3,将它沿⊙O的圆周作无滑动的滚动,当它第n次回到起始位置时,点I所经过的路径长为 (请用含n的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了解本校学生平均每天的课外做作业的时间情况,随机抽取部分学生进行问卷调查,并将调查的结果分为A、B、C、D四个等级(设做作业时间为t小时,A:t<1;B:1≤t<1.5;C:1.5≤t<2;D:t≥2)根据调查结果绘成了如下两幅不完整的统计图.
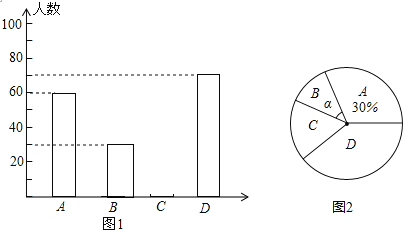
请根据图中信息,解答下列问题:
(1)本次调查中,抽取的学生人数是 ;
(2)图2中α的度数是 ,并补全图1条形统计图;
(3)该校共有2800名学生名,请估计作业时间不少于2小时的人数为 ;
(4)在此次调查中,甲班有2人平均每天的作业时间超过2小时,乙班有3名学生平均每天作业时间超过2小时,现从这5人中选取2人参加座谈会,请用树状图或列表的方法,求出“所选的2人来自不同班级”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市试销一种成本价为80元/瓶的白酒,规定试销期间单价不低于100元/瓶且不高于160元/瓶.经试销发现,销售量y(瓶)与销售单价x(元/瓶)符合一次函数关系,且x=120时,y=100;x=130时,y=95.
(1)求y与x的函数关系式,并写出自变量x的取值范围;
(2)当销售单价x定为每瓶多少元时,销售利润(w)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,等边△OAB的顶点B的坐标为(2,0),点A在第一象限内,将△OAB沿直线OA的方向平移至△O′A′B′的位置,此时点A′的横坐标为3,则点B′的坐标为( )
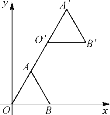
A. (4,2![]() ) B. (3,3) C. (4,3) D. (3,2)
) B. (3,3) C. (4,3) D. (3,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
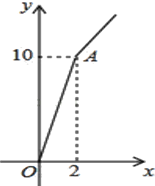
【题目】“十九大”之后,某种子站让利给农民,对价格为a元/千克的种子,如果一次购买2千克以上的,超过2千克部分的种子价格打8折.某科技人员对付款金额和购买量这两个变量的对应关系用列表法做了分析,并绘制出了函数图象.以下是该科技人员绘制的图象和表格的不完整资料,已知点A的坐标为(2,10).请你结合表格和图象:
付款金额(元) | a | 7.5 | 10 | 12 | b |
购买量(千克) | 1 | 1.5 | 2 | 2.5 | 3 |
(1)、指出付款金额和购买量哪个变量是函数的自变量x,并写出表中a、b的值;
(2)、求出当x>2时,y关于x的函数解析式;
(3)、甲农户将8.8元钱全部用于购买该玉米种子,乙农户购买了4165克该玉米种子,分别计算他们的购买量和付款金额.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com