【题目】某超市试销一种成本价为80元/瓶的白酒，规定试销期间单价不低于100元/瓶且不高于160元/瓶．经试销发现，销售量y（瓶）与销售单价x（元/瓶）符合一次函数关系，且x=120时，y=100；x=130时，y=95．
（1）求y与x的函数关系式，并写出自变量x的取值范围；
（2）当销售单价x定为每瓶多少元时，销售利润（w）最大？最大利润是多少？
【答案】（1）y=﹣
x+160，（100≤x≤160）；（2）：当销售单价x定为每瓶160元时，销售利润最大，最大利润是6400元．
【解析】试题分析：（1）待定系数法求解可得；
（2）根据“总利润=单件利润×销售量”列出函数解析式并配方，结合二次函数的性质即可得出函数的最值．
试题解析：解：（1）设一次函数的解析式为y=kx+b，依题意有：
，解得：
，∴y与x的函数关系式为y=﹣x+160，（100≤x≤160）；
（2）依题意有：W=（x﹣80）（﹣x+160）=﹣（x﹣200）2+7200．∵a=﹣＜0，∴当x＜200时，y随x的增大而增大，∴当x=160时，W有最大值，最大值为6400元．
答：当销售单价x定为每瓶160元时，销售利润最大，最大利润是6400元．
阳光同学一线名师全优好卷系列答案科目：初中数学 来源： 题型：
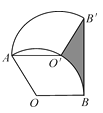
【题目】如图，将半径为2，圆心角为120°的扇形OAB绕点A逆时针旋转60°，点O，B的对应点分别为O′，B′，连接BB′，则图中阴影部分的面积是 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
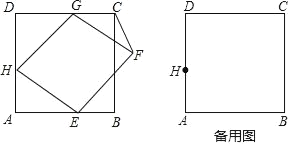
【题目】如图，已知正方形ABCD的边长为3，菱形EFGH的三个顶点E、G、H分别在正方形的边AB、CD、DA上，AH＝1，联结CF．
（1）当DG＝1时，求证：菱形EFGH为正方形；
（2）设DG＝x，△FCG的面积为y，写出y关于x的函数解析式，并指出x的取值范围；
（3）当DG＝
时，求∠GHE的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
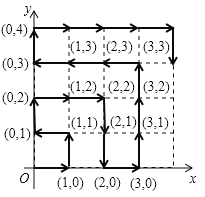
【题目】在平面直角坐标系中，有若干个横纵坐标分别为整数的点，其顺序按图中“→”方向排列，其对应的点坐标依次为
，
，
，
，
，
，
，
…，根据这个规律，第2018个横坐标为（ ）
A.44B.45C.46D.47
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，抛物线L：y=ax2+bx+c与x轴交于A、B（3，0）两点（A在B的左侧），与y轴交于点C（0，3），已知对称轴x=1．
（1）求抛物线L的解析式；
（2）将抛物线L向下平移h个单位长度，使平移后所得抛物线的顶点落在△OBC内（包括△OBC的边界），求h的取值范围；
（3）设点P是抛物线L上任一点，点Q在直线l：x=﹣3上，△PBQ能否成为以点P为直角顶点的等腰直角三角形？若能，求出符合条件的点P的坐标；若不能，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：点P（m，4）在反比例函数y=
的图象上，正比例函数的图象经过点P和点Q（6，n）．
（1）求正比例函数的解析式；
（2）在x轴上求一点M，使△MPQ的面积等于18．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义：如果一个分式能化成一个整式与一个分子为常数的分式的和的形式，则称这个分式为“和谐分式”．如：
，则
是“和谐分式”．
(1)下列分式中，属于“和谐分式”的是_____(填序号)；
①
；②
；③
；④
；
(2)将“和谐分式”
化成一个整式与一个分子为常数的分式的和的形式为：＝_______(要写出变形过程)；
(3)应用：先化简
，并求x取什么整数时，该式的值为整数．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
