
【题目】已知:点P(m,4)在反比例函数y=![]() 的图象上,正比例函数的图象经过点P和点Q(6,n).
的图象上,正比例函数的图象经过点P和点Q(6,n).
(1)求正比例函数的解析式;
(2)在x轴上求一点M,使△MPQ的面积等于18.
【答案】(1)正比例函数的解析式为y=![]() x;(2)点M的坐标为(﹣9,0)或(9,0).
x;(2)点M的坐标为(﹣9,0)或(9,0).
【解析】试题分析:(1)设正比例函数解析式为y=kx(k≠0),把点P的坐标代入反比例函数解析式求出m的值,从而得到点P的坐标,然后代入正比例函数解析式求解即可;
(2)把点Q的坐标代入正比例函数解析式求出n,根据S△MPQ=S△QOM﹣S△POM,列式求出OM的长,再分点M在原点的左侧与右侧两种情况讨论求解.
试题解析:解:(1)设正比例函数解析式为y=kx(k≠0).∵点P(m,4)在反比例函数y=![]() 的图象上,∴
的图象上,∴![]() =4,解得:m=3,∴P的坐标为(3,4).∵正比例函数图象经过点P,∴3k=4,解得:k=
=4,解得:m=3,∴P的坐标为(3,4).∵正比例函数图象经过点P,∴3k=4,解得:k=![]() ,∴正比例函数的解析式为y=
,∴正比例函数的解析式为y=![]() x;
x;
(2)∵正比例函数图象经过点Q(6,n),∴n=![]() ×6=8,∴点Q(6,8),∴S△MPQ=S△QOM﹣S△POM=
×6=8,∴点Q(6,8),∴S△MPQ=S△QOM﹣S△POM=![]() OM8﹣
OM8﹣![]() OM4=2OM.∵△MPQ的面积等于18,∴2OM=18,解得:OM=9,点M在原点左边时,点M(﹣9,0),点M在原点右边时,点M(9,0).
OM4=2OM.∵△MPQ的面积等于18,∴2OM=18,解得:OM=9,点M在原点左边时,点M(﹣9,0),点M在原点右边时,点M(9,0).
综上所述:点M的坐标为(﹣9,0)或(9,0).


科目:初中数学 来源: 题型:
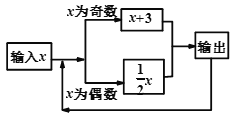
【题目】如图,是某一计算程序,回答如下问题:
(1)当输入某数后,第一次得到的结果为5,则输入的数值x=_______;
(2)若输入的x的值为16时,第1次得到的结果为8,第2次得到的结果为4,…,则第2019次得到的结果是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市试销一种成本价为80元/瓶的白酒,规定试销期间单价不低于100元/瓶且不高于160元/瓶.经试销发现,销售量y(瓶)与销售单价x(元/瓶)符合一次函数关系,且x=120时,y=100;x=130时,y=95.
(1)求y与x的函数关系式,并写出自变量x的取值范围;
(2)当销售单价x定为每瓶多少元时,销售利润(w)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,等边△OAB的顶点B的坐标为(2,0),点A在第一象限内,将△OAB沿直线OA的方向平移至△O′A′B′的位置,此时点A′的横坐标为3,则点B′的坐标为( )
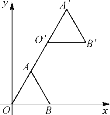
A. (4,2![]() ) B. (3,3) C. (4,3) D. (3,2)
) B. (3,3) C. (4,3) D. (3,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y是x的一次函数,当x=1时,y=1;当x=-2时,y=-14.
(1)求这个一次函数的关系式;
(2)在如图所示的平面直角坐标系中作出函数的图像;
(3)由图像观察,当0≤x≤2时,函数y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y1=2x-2的图像与y轴交于点A,直线y2=-2x+6的图像与y轴交于点B,两者相交于点C.
(1)方程组![]() 的解是______;
的解是______;
(2)当y1>0与y2>0同时成立时,x的取值范围为_____;
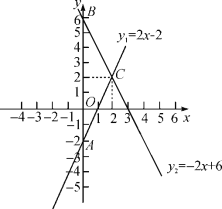
(3)求△ABC的面积;
(4)在直线y1=2x-2的图像上存在异于点C的另一点P,使得△ABC与△ABP的面积相等,请求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
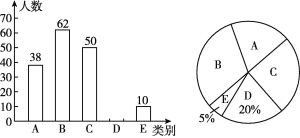
【题目】某品牌牛奶供应商提供A,B,C,D,E五种不同口味的牛奶供学生选择.某校为了了解学生对不同口味的牛奶的喜好,对全校订牛奶的学生进行了随机调查,并根据调查结果绘制了如图所示两幅不完整的统计图.请根据统计图中的信息,解答下列问题:
(1)本次调查的学生有多少名?
(2)补全条形统计图,并计算出喜好C口味牛奶的学生人数对应的扇形圆心角的度数.
(3)该校共有1 200名学生订了该品牌的牛奶,牛奶供应商每天只为每名订牛奶的学生配送一盒牛奶,要使学生每天都能喝到自己喜好的品味的牛奶,牛奶供应商每天送往该校的牛奶中,B口味牛奶要比C口味牛奶约多送多少盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
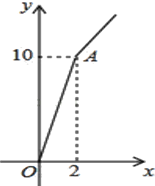
【题目】“十九大”之后,某种子站让利给农民,对价格为a元/千克的种子,如果一次购买2千克以上的,超过2千克部分的种子价格打8折.某科技人员对付款金额和购买量这两个变量的对应关系用列表法做了分析,并绘制出了函数图象.以下是该科技人员绘制的图象和表格的不完整资料,已知点A的坐标为(2,10).请你结合表格和图象:
付款金额(元) | a | 7.5 | 10 | 12 | b |
购买量(千克) | 1 | 1.5 | 2 | 2.5 | 3 |
(1)、指出付款金额和购买量哪个变量是函数的自变量x,并写出表中a、b的值;
(2)、求出当x>2时,y关于x的函数解析式;
(3)、甲农户将8.8元钱全部用于购买该玉米种子,乙农户购买了4165克该玉米种子,分别计算他们的购买量和付款金额.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在同一平面内四个点A,B,C,D.
(1)利用尺规,按下面的要求作图.要求:不写画法,保留作图痕迹,不必写结论.
①作射线AC;
②连接AB,BC,BD,线段BD与射线AC相交于点O;
③在线段AC上作一条线段CF,使CF=AC﹣BD.
(2)观察(1)题得到的图形,我们发现线段AB+BC>AC,得出这个结论的依据是 .
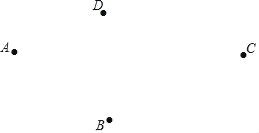
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com