
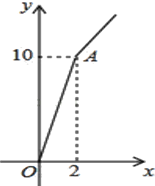
【题目】“十九大”之后,某种子站让利给农民,对价格为a元/千克的种子,如果一次购买2千克以上的,超过2千克部分的种子价格打8折.某科技人员对付款金额和购买量这两个变量的对应关系用列表法做了分析,并绘制出了函数图象.以下是该科技人员绘制的图象和表格的不完整资料,已知点A的坐标为(2,10).请你结合表格和图象:
付款金额(元) | a | 7.5 | 10 | 12 | b |
购买量(千克) | 1 | 1.5 | 2 | 2.5 | 3 |
(1)、指出付款金额和购买量哪个变量是函数的自变量x,并写出表中a、b的值;
(2)、求出当x>2时,y关于x的函数解析式;
(3)、甲农户将8.8元钱全部用于购买该玉米种子,乙农户购买了4165克该玉米种子,分别计算他们的购买量和付款金额.
【答案】(1)a=5,b=14;(2)y=4x+2;(3) 18.66元
【解析】分析:分析:(1)根据函数图象可得:购买量是函数的自变量x,也可看出2千克的金额为10元,从而可求1千克的价格,即a的值,由表格可得出:当购买量大于等于2千克时,购买量每增加0.5千克,价格增加2元,进而可求b的值;(2)先设关系式为y=px+q,然后将(2,10),且x=3时,y=14,代入关系式即可求出p,q的值,从而确定关系式;(3)当y=8.8时,单价为5元,此时购买量为8.8÷5,然后将x=4.165代入关系式计算相应的y值.
本题解析:
解:(1)购买量是函数中的自变量x,
设射线OA解析式为![]() ,
,
把![]() 代入得:
代入得:![]() ,即
,即![]() ,
,![]() 射线OA解析式为
射线OA解析式为![]() ,
,
把![]() 代入得:
代入得:![]() ,即
,即![]() ;
;
根据题意得:![]() ;
;
(2)当![]() 时,设y与x的函数关系式为:
时,设y与x的函数关系式为:![]() ,
,![]() 经过点
经过点![]() ,
,
又![]() 时,
时,![]() ,
, ,
,
解得: ,
,
∴当![]() 时,y与x的函数关系式为:
时,y与x的函数关系式为:![]() ;
;
(3)当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
∴甲农户的购买量为1.76千克,乙农户的付款金额为18.66元.


科目:初中数学 来源: 题型:
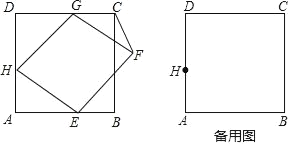
【题目】如图,已知正方形ABCD的边长为3,菱形EFGH的三个顶点E、G、H分别在正方形的边AB、CD、DA上,AH=1,联结CF.
(1)当DG=1时,求证:菱形EFGH为正方形;
(2)设DG=x,△FCG的面积为y,写出y关于x的函数解析式,并指出x的取值范围;
(3)当DG=![]() 时,求∠GHE的度数.
时,求∠GHE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点P(m,4)在反比例函数y=![]() 的图象上,正比例函数的图象经过点P和点Q(6,n).
的图象上,正比例函数的图象经过点P和点Q(6,n).
(1)求正比例函数的解析式;
(2)在x轴上求一点M,使△MPQ的面积等于18.
查看答案和解析>>
科目:初中数学 来源: 题型:
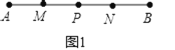
【题目】如图,点P是线段AB上的一点,点M、N分别是线段AP、PB的中点.
(1)如图1,若点P是线段AB的中点,且MP=4cm,求线段AB的长;
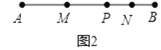
(2)如图2,若点P是线段AB上的任一点,且AB=12cm,求线段MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 阅读下列材料:我们知道
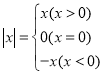
现在我们可以用这个结论来化简含有绝对值的代数式,如化简代数式![]() 时,令
时,令![]() ,求得
,求得![]() ;令
;令![]() ,求得
,求得![]() (称-1,2分别为
(称-1,2分别为![]() ,
,![]() 的零点值).在有理数范围内,零点值-1和2可将全体有理数分成不重复且不遗漏的如下3种情况:
的零点值).在有理数范围内,零点值-1和2可将全体有理数分成不重复且不遗漏的如下3种情况:
①当![]() 时,原式
时,原式![]() ;
;
②当![]() 时,原式
时,原式![]() ;
;
③当![]() 时,原式
时,原式![]() .
.
综上所述,
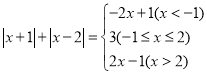
通过以上阅读,请你解决以下问:
(1)分别求出![]() 和
和![]() 的零点值;
的零点值;
(2)化简代数式![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠CAB=30°, AC=4.5cm. M是边AC上的一个动点,连接MB,过点M作MB的垂线交AB于点N. 设AM=x cm,AN=y cm.(当点M与点A或点C重合时,y的值为0)
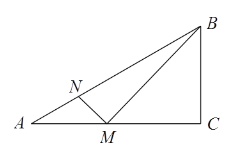
探究函数y随自变量x的变化而变化的规律.
(1) 通过取点、画图、测量,得到了x与y的几组对应值,如下表:
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 |
y/cm | 0 | 0.4 | 0.8 | 1.2 | 1.6 | 1.7 | 1.6 | 1.2 | 0 |
(要求:补全表格,相关数值保留一位小数)
(2)建立平面直角坐标系xOy,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(3)结合画出的函数图象,解决问题:当AN=![]() AM时,AM的长度约为 cm(结果保留一位小数).
AM时,AM的长度约为 cm(结果保留一位小数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一个分式能化成一个整式与一个分子为常数的分式的和的形式,则称这个分式为“和谐分式”.如:![]() ,则
,则![]() 是“和谐分式”.
是“和谐分式”.
(1)下列分式中,属于“和谐分式”的是_____(填序号);
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;
;
(2)将“和谐分式”![]() 化成一个整式与一个分子为常数的分式的和的形式为:
化成一个整式与一个分子为常数的分式的和的形式为:![]() =_______(要写出变形过程);
=_______(要写出变形过程);
(3)应用:先化简![]() ,并求x取什么整数时,该式的值为整数.
,并求x取什么整数时,该式的值为整数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的四个顶点分别在反比例函数![]() 与
与![]() (x>0,0<m<n)的图象上,对角线BD//y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(x>0,0<m<n)的图象上,对角线BD//y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(1)当m=4,n=20时.
①若点P的纵坐标为2,求直线AB的函数表达式.
②若点P是BD的中点,试判断四边形ABCD的形状,并说明理由.
(2)四边形ABCD能否成为正方形?若能,求此时m,n之间的数量关系;若不能,试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
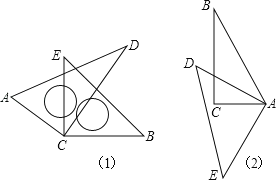
【题目】(1)如图(1),将两块直角三角尺叠放在一起,并且它们的直角顶点C重合,请比较∠ACE和∠DCB的大小,并说明理由;
(2)如图(2),若是将等腰直角三角尺的直角顶点和另一把直角三角尺的60°角的顶点A重合,将三角板ADE绕点A旋转,旋转过程中三角板ADE的边AD始终在∠BAC的内部,试探索:在旋转过程中,∠CAE与∠BAD的差是否发生变化?若不变,请求出这个差值;若变化,请求出差的变化范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com