
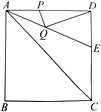
【题目】如图,正方形![]() 的边长是
的边长是![]() ,
,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,若点
,若点![]() 分别是
分别是![]() 和
和![]() 上的动点,则
上的动点,则![]() 的最小值是_______.
的最小值是_______.
【答案】![]()
【解析】
过D作AE的垂线交AE于F,交AC于D′,再过D′作D′P′⊥AD,由角平分线的性质可得出D′是D关于AE的对称点,进而可知D′P′即为DQ+PQ的最小值.
解:解:作D关于AE的对称点D′,再过D′作D′P′⊥AD于P′,
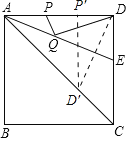
∵DD′⊥AE,
∴∠AFD=∠AFD′,
∵AF=AF,∠DAE=∠CAE,
∴△DAF≌△D′AF,
∴D′是D关于AE的对称点,AD′=AD=5,
∴D′P′即为DQ+PQ的最小值,
∵四边形ABCD是正方形,
∴∠DAD′=45°,
∴AP′=P′D′,
∴在Rt△AP′D′中,
P′D′2+AP′2=AD′2,AD′2=25,
∵AP′=P′D',
2P′D′2=AD′2,即2P′D′2=25,
![]() ,即DQ+PQ的最小值为
,即DQ+PQ的最小值为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后,折叠DE分别交AB、AC于E、G,连接GF,下列结论:①∠FGD=112.5°②BE=2OG③S△AGD=S△OGD④四边形AEFG是菱形( )
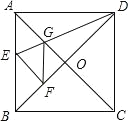
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校要从小王和小李两名同学中挑选一人参加全市知识竞赛,在最近的五次选拔测试中,他俩的成绩分别如下表:
次数 | 1 | 2 | 3 | 4 | 5 |
小王 | 60 | 75 | 100 | 90 | 75 |
小李 | 70 | 90 | 100 | 80 | 80 |
根据上表解答下列问题:
(1)完成下表:
姓名 | 平均成绩(分) | 中位数(分) | 众数(分) | 方差 |
小王 | 80 | 75 | 75 | 190 |
小李 |
(2)在这五次测试中,成绩比较稳定的同学是谁?若将80分以上(含80分)的成绩视为优秀,则小王、小李在这五次测试中的优秀率各是多少?
(3)历届比赛表明,成绩达到80分以上(含80分)就很可能获奖,成绩达到90分以上(含90分)就很可能获得一等奖,那么你认为选谁参加比赛比较合适?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
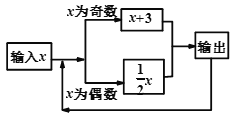
【题目】如图,是某一计算程序,回答如下问题:
(1)当输入某数后,第一次得到的结果为5,则输入的数值x=_______;
(2)若输入的x的值为16时,第1次得到的结果为8,第2次得到的结果为4,…,则第2019次得到的结果是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
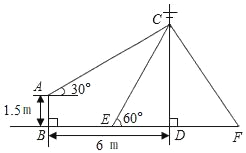
【题目】如图,在电线杆CD上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆6m的B处安置高为1.5m的测角仪AB,在A处测得电线杆上C处的仰角为30°,求拉线CE的长.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了改善教室空气环境,某校九年级1班班委会计划到朝阳花卉基地购买绿植.已知该基地一盆绿萝与一盆吊兰的价格之和是12元.班委会决定用60元购买绿萝,用90元购买吊兰,所购绿萝数量正好是吊兰数量的两倍.
(1)分别求出每盆绿萝和每盆吊兰的价格;
(2)该校九年级所有班级准备一起到该基地购买绿萝和吊兰共计90盆,其中绿萝数量不超过吊兰数量的一半,该基地特地对吊兰价格给出了如下的优惠政策,一次性购买的吊兰超过20盆时,超过部分的吊兰每盆的价格打8折,根据该基地的优惠信息,九年级购买这两种绿植各多少盆时总费用最少?最少费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,等边△ABC的边长为3,分别以顶点B、A、C为圆心,BA长为半径作![]() 、
、![]() 、
、![]() ,我们把这三条弧所组成的图形称作莱洛三角形,显然莱洛三角形仍然是轴对称图形,设点l为对称轴的交点.
,我们把这三条弧所组成的图形称作莱洛三角形,显然莱洛三角形仍然是轴对称图形,设点l为对称轴的交点.
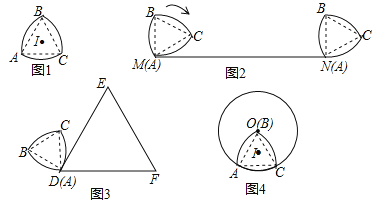
(1)如图2,将这个图形的顶点A与线段MN作无滑动的滚动,当它滚动一周后点A与端点N重合,则线段MN的长为 ;
(2)如图3,将这个图形的顶点A与等边△DEF的顶点D重合,且AB⊥DE,DE=2π,将它沿等边△DEF的边作无滑动的滚动当它第一次回到起始位置时,求这个图形在运动过程中所扫过的区域的面积;
(3)如图4,将这个图形的顶点B与⊙O的圆心O重合,⊙O的半径为3,将它沿⊙O的圆周作无滑动的滚动,当它第n次回到起始位置时,点I所经过的路径长为 (请用含n的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市试销一种成本价为80元/瓶的白酒,规定试销期间单价不低于100元/瓶且不高于160元/瓶.经试销发现,销售量y(瓶)与销售单价x(元/瓶)符合一次函数关系,且x=120时,y=100;x=130时,y=95.
(1)求y与x的函数关系式,并写出自变量x的取值范围;
(2)当销售单价x定为每瓶多少元时,销售利润(w)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
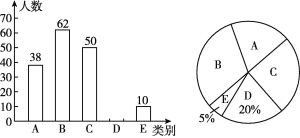
【题目】某品牌牛奶供应商提供A,B,C,D,E五种不同口味的牛奶供学生选择.某校为了了解学生对不同口味的牛奶的喜好,对全校订牛奶的学生进行了随机调查,并根据调查结果绘制了如图所示两幅不完整的统计图.请根据统计图中的信息,解答下列问题:
(1)本次调查的学生有多少名?
(2)补全条形统计图,并计算出喜好C口味牛奶的学生人数对应的扇形圆心角的度数.
(3)该校共有1 200名学生订了该品牌的牛奶,牛奶供应商每天只为每名订牛奶的学生配送一盒牛奶,要使学生每天都能喝到自己喜好的品味的牛奶,牛奶供应商每天送往该校的牛奶中,B口味牛奶要比C口味牛奶约多送多少盒?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com