
【题目】涟水外卖市场竞争激烈,美团、饿了么等公司订单大量增加,某公司负责招聘外卖送餐员,具体方案如下:每月不超出750单,每单收入4元;超出750单的部分每单收入m元.
(1)若某“外卖小哥”某月送了500单,收入 元;
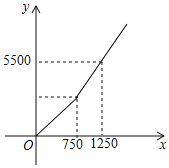
(2)若“外卖小哥”每月收入为y(元),每月送单量为x单,y与x之间的关系如图所示,求y与x之间的函数关系式;
(3)若“外卖小哥”甲和乙在某个月内共送单1200单,且甲送单量低于乙送单量,共收入5000元,问:甲、乙送单量各是多少?
【答案】(1)2000;(2)y=5x﹣750;(3)甲送250单,乙送950单
【解析】
(1)根据题意可以求得“外卖小哥”某月送了500单的收入情况;
(2)分段函数,运用待定系数法解答即可;
(3)根据题意,利用分类讨论的方法可以求得甲、乙送单量各是多少.
解:(1)由题意可得,
“外卖小哥”某月送了500单,收入为:4×500=2000元,
故答案为:2000;
(2)当0≤x<750时,y=4x
当x≥750时,
当x=4时,y=3000
设y=kx+b,根据题意得![]() ,
,
解得![]() ,
,
∴y=5x﹣750;
(3)设甲送a单,则a<600<750,
则乙送(1200﹣a)单,
若1200﹣a<750,则4a+4(1200﹣a)=4800≠5000,不合题意,
∴1200﹣a>750,
∴4a+5(1200﹣a)﹣750=5000,
∴a=250,
1200﹣a=950,
故甲送250单,乙送950单.


科目:初中数学 来源: 题型:
【题目】2019年北疆承办了世界园艺博览会,某商店为了抓住博览会的商机,决定购买A.B两种世园会纪念品,若购进A中纪念品20件,B种纪念品10件,需要2000元;若购进A中纪念品8件,B种纪念品6件,需要1100元.
(1)求购进A.B两种纪念品每件各需要多少元?
(2)若该商店决定拿出10000元全部用来购进这两种纪念品,考虑到市场需求,要求购进A种纪念品的数量不少于B种的6倍,且少于B种纪念品数量的8倍,设购进B种纪念品a件,则该商店共有几种进货方案?
(3)在第(2)问的条件下,若销售每件A种纪念品可获利润30元,每件B种纪念品可获利润40元,设总利润为y元,请写出总利润y(元)与a(个)的函数关系式,并根据函数关系式说明总利润最高时的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
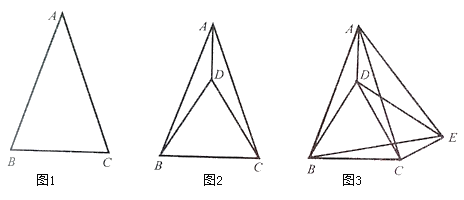
【题目】如图1,张老师在黑板上画出了一个![]() ,其中
,其中![]() ,让同学们进行探究.
,让同学们进行探究.
(1)探究一:
如图2,小明以![]() 为边在
为边在![]() 内部作等边
内部作等边![]() ,连接
,连接![]() ,请直接写出
,请直接写出![]() 的度数_____________;
的度数_____________;
(2)探究二:
如图3,小彬在(1)的条件下,又以![]() 为边作等边
为边作等边![]() ,连接
,连接![]() .判断
.判断![]() 与
与![]() 的数量关系;并说明理由;
的数量关系;并说明理由;
(3)探究三:
如图3,小聪在(2)的条件下,连接![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边![]() 和等腰
和等腰![]() ,
,![]() ,
,![]() .
.
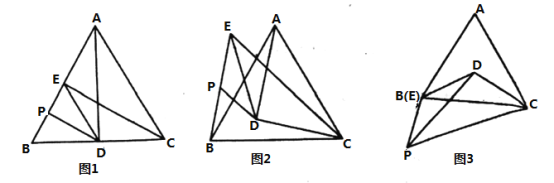
(1)如图1,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,
上,![]() 是
是![]() 的中点,连接
的中点,连接![]() ,
,![]() ,则线段
,则线段![]() 与
与![]() 之间的数量关系为 ;
之间的数量关系为 ;
(2)如图2,点![]() 在
在![]() 内部,点
内部,点![]() 在
在![]() 外部,
外部,![]() 是
是![]() 的中点,连接
的中点,连接![]() ,
,![]() ,则(1)中的结论是否仍然成立?若成立,请给出证明,若不成立,请说明理由.
,则(1)中的结论是否仍然成立?若成立,请给出证明,若不成立,请说明理由.
(3)如图3,若点![]() 在
在![]() 内部,点
内部,点![]() 和点
和点![]() 重合,点
重合,点![]() 在
在![]() 下方,且
下方,且![]() 为定值,当
为定值,当![]() 最大时,
最大时,![]() 的度数为 .
的度数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,图形G上点P(x,y)的纵坐标y与其横坐标x的差y-x称为P点的“坐标差”,而图形G上所有点的“坐标差”中的最大值称为图形G的“特征值”
(1)①点A(1,3) 的“坐标差”为 。
②抛物线y=-x2+3x+3的“特征值”为 。
(2)某二次函数y=-x2+bx+c(c≠0) 的“特征值”为1,点B(m,0)与点C分别是此二次函数的图象与x轴和y轴的交点,且点B与点C的“坐标差”相等。
①直接写出m= (用含c的式子表示)
②求此二次函数的表达式。
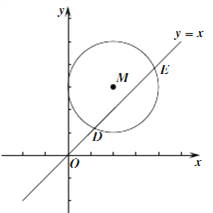
(3)如图,在平面直角坐标系xOy中,以M(2,3)为圆心,2为半径的圆与直线y=x相交于点D、E请直接写出⊙M的“特征值”为 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,∠ACB=90°,D为BC的中点,DE⊥AB,垂足为E,过点B作BF∥AC交DE的延长线于点F,连接CF.
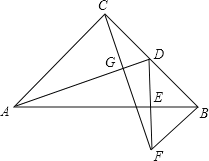
(1)求证:CD=BF;
(2)求证:AD⊥CF;
(3)连接AF,试判断△ACF的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() ,二次函数
,二次函数![]() (其中m>4).
(其中m>4).
(1)求二次函数图象的顶点坐标(用含m的代数式表示);
(2)利用函数图象解决下列问题:
①若![]() ,求当
,求当![]() 且
且![]() ≤0时,自变量
≤0时,自变量![]() 的取值范围;
的取值范围;
②如果满足![]() 且
且![]() ≤0时自变量
≤0时自变量![]() 的取值范围内有且只有一个整数,直接写出
的取值范围内有且只有一个整数,直接写出![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在宽20米,长32米的矩形耕地上,修筑同样宽的三条路(两条纵向,一条横向,并且横向与纵向互相垂直),把这块耕地分成大小相等的六块试验田,要使试验田的面积是570平方米,问道路应该多宽?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com