
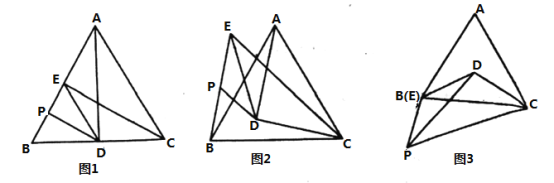
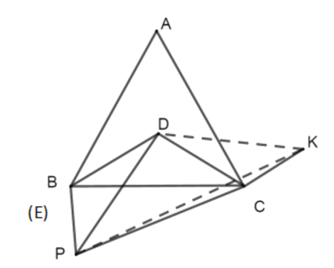
【题目】已知等边![]() 和等腰
和等腰![]() ,
,![]() ,
,![]() .
.
(1)如图1,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,
上,![]() 是
是![]() 的中点,连接
的中点,连接![]() ,
,![]() ,则线段
,则线段![]() 与
与![]() 之间的数量关系为 ;
之间的数量关系为 ;
(2)如图2,点![]() 在
在![]() 内部,点
内部,点![]() 在
在![]() 外部,
外部,![]() 是
是![]() 的中点,连接
的中点,连接![]() ,
,![]() ,则(1)中的结论是否仍然成立?若成立,请给出证明,若不成立,请说明理由.
,则(1)中的结论是否仍然成立?若成立,请给出证明,若不成立,请说明理由.
(3)如图3,若点![]() 在
在![]() 内部,点
内部,点![]() 和点
和点![]() 重合,点
重合,点![]() 在
在![]() 下方,且
下方,且![]() 为定值,当
为定值,当![]() 最大时,
最大时,![]() 的度数为 .
的度数为 .
【答案】(1)![]()
![]() ;
;
(2)成立,理由见解析;
(3)![]()
【解析】
(1)根据等边三角形的性质,![]() ,
,![]() ,可得
,可得![]() 是等边三角形,
是等边三角形,![]() 是
是![]() 的中点,利用等边三角形三线合一性质,以及
的中点,利用等边三角形三线合一性质,以及![]() 得出
得出![]() ,所以PD是
,所以PD是![]() 中位线,得出点D是BC的中点,AD=CE,可得出结论
中位线,得出点D是BC的中点,AD=CE,可得出结论![]()
![]() .
.
(2)作辅助线,延长ED到F,使得![]() ,使得
,使得![]() 是等边三角形,PD是
是等边三角形,PD是![]() 的中位线,通过证明三角形全等得出
的中位线,通过证明三角形全等得出![]() 可证明结论.
可证明结论.
(3)作出等腰![]() ,由旋转模型证明三角形
,由旋转模型证明三角形![]() ,利用P、C、K三点共线时,PK最大,即PD最大可求解得.
,利用P、C、K三点共线时,PK最大,即PD最大可求解得.
(1)根据图1,在等边![]() 和等腰
和等腰![]() 中,
中,
![]()
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]()
![]() 是
是![]() 的中点,
的中点,
![]() ,
,
![]() ,
,![]() ,
,
![]() PD是
PD是![]() 中位线
中位线
![]() 分别是
分别是![]() 的中点,
的中点,
![]() ,
,
故答案为:![]()
![]() .
.
(2)结论成立.
理由:如下图中,延长ED到F,使得![]() ,连接FC,BF,
,连接FC,BF,
![]() ,
,
![]()
![]()
![]()
![]()
![]() 是等边三角形,
是等边三角形,
![]() ,
,
在![]() 和
和![]() 中
中
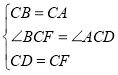
![]()
![]() ,
,
![]() ,
,
![]() ,
,
故答案为:结论成立;
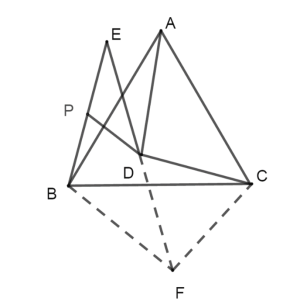
(3)作![]() ,且
,且![]() ,
,
连接PK,DK,
则![]() 为等腰三角形,
为等腰三角形,
在![]() 和
和![]() 中
中
![]() ,
,
![]() ,
,
即![]() 为定值.
为定值.
P、C、K三点共线时,PK最大,即PD最大,
![]() 此时,
此时,![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】已知A,B两地相距120千米,甲乙两人沿同一条公路匀速行驶,甲骑自行车以20千米/时从A地前往B地,同时乙骑摩托车从B地前往A地,设两人之间的距离为s(千米),甲行驶的时间为t(小时),若s与t的函数关系如图所示,则下列说法错误的是( )
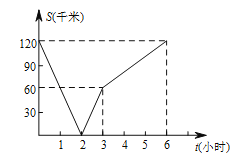
A.经过2小时两人相遇
B.若乙行驶的路程是甲的2倍,则t=3
C.当乙到达终点时,甲离终点还有60千米
D.若两人相距90千米,则t=0.5或t=4.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“一带一路”战略的影响下,某茶叶经销商准备把“茶路”融入“丝路”,经计算,他销售10斤A级别和20斤B级别茶叶的利润为4000元,销售20斤A级别和10斤B级别茶叶的利润为3500元
(1)分别求出每斤A级别茶叶和每斤B级别茶叶的销售利润;
(2)若该经销商一次购进两种级别的茶叶共200斤用于出口.设购买A级别茶叶a斤(70≤a≤120),销售完A、B两种级别茶叶后获利w元.
①求出w与a之间的函数关系式;
②该经销商购进A、B两种级别茶叶各多少斤时,才能获取最大的利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“作圆的内接正方形”的尺规作图过程。
已知:⊙O.
求作:圆的内接正方形.
如图,
(1)过圆心O作直线AC,与⊙O相交于A,C两点;
(2)过点O作直线BD⊥AC,交⊙O于B,D两点;
(3)连接AB,BC,CD,DA。
∴四边形ABCD为所求。

请回答:该尺规作图的依据是____________________________。(写出两条)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班数学兴趣小组对不等式组![]() ,讨论得到以下结论:①若a=5,则不等式组的解集为3<x≤5;②若a=2,则不等式组无解;③若不等式组无解,则a的取值范围为a<3;④若不等式组只有两个整数解,则a的值可以为5.1,其中,正确的结论的序号是____.
,讨论得到以下结论:①若a=5,则不等式组的解集为3<x≤5;②若a=2,则不等式组无解;③若不等式组无解,则a的取值范围为a<3;④若不等式组只有两个整数解,则a的值可以为5.1,其中,正确的结论的序号是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】涟水外卖市场竞争激烈,美团、饿了么等公司订单大量增加,某公司负责招聘外卖送餐员,具体方案如下:每月不超出750单,每单收入4元;超出750单的部分每单收入m元.
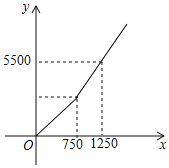
(1)若某“外卖小哥”某月送了500单,收入 元;
(2)若“外卖小哥”每月收入为y(元),每月送单量为x单,y与x之间的关系如图所示,求y与x之间的函数关系式;
(3)若“外卖小哥”甲和乙在某个月内共送单1200单,且甲送单量低于乙送单量,共收入5000元,问:甲、乙送单量各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△![]() 和△
和△![]() 中,
中,![]() ,
,![]() 和
和![]() 分别为
分别为![]() 边和
边和![]() 边上的中线,再从以下三个条件:①
边上的中线,再从以下三个条件:①![]() ;②
;②![]() ;③
;③![]() 中任取两个为已知条件,另一个为结论,则最多可以构成_______个正确的命题.
中任取两个为已知条件,另一个为结论,则最多可以构成_______个正确的命题.
查看答案和解析>>
科目:初中数学 来源: 题型:
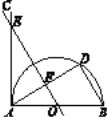
【题目】已知:如图, ![]() 是半圆
是半圆![]() 的直径,D是半圆上的一个动点(点D不与点A,B 重合),
的直径,D是半圆上的一个动点(点D不与点A,B 重合), ![]()
(1)求证:AC是半圆![]() 的切线;
的切线;

(2)过点O作BD的平行线,交AC于点E,交AD于点F,且EF=4, AD=6, 求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.填空:
①∠AEB的度数为______;
②线段AD,BE之间的数量关系为______.
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com