
【题目】已知A,B两地相距120千米,甲乙两人沿同一条公路匀速行驶,甲骑自行车以20千米/时从A地前往B地,同时乙骑摩托车从B地前往A地,设两人之间的距离为s(千米),甲行驶的时间为t(小时),若s与t的函数关系如图所示,则下列说法错误的是( )
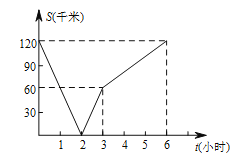
A.经过2小时两人相遇
B.若乙行驶的路程是甲的2倍,则t=3
C.当乙到达终点时,甲离终点还有60千米
D.若两人相距90千米,则t=0.5或t=4.5
【答案】B
【解析】
由图象得到经过2小时两人相遇,A选项正确,由于乙的速度是![]() =40千米/时,乙的速度是甲的速度的2倍可知B选项错误,计算出乙到达终点时,甲走的路程,可得C选项正确,当0<t≤2时,得到t=0.5,当3<t≤6时,得到t=4.5,于是得到若两人相距90千米,则t=0.5或t=4.5,故D正确.
=40千米/时,乙的速度是甲的速度的2倍可知B选项错误,计算出乙到达终点时,甲走的路程,可得C选项正确,当0<t≤2时,得到t=0.5,当3<t≤6时,得到t=4.5,于是得到若两人相距90千米,则t=0.5或t=4.5,故D正确.
由图象知:经过2小时两人相遇,A选项正确;
甲的速度是20千米/小时,则乙的速度是![]() =40千米/时,乙的速度是甲的速度的2倍,所以在乙到达终点之前,乙行驶的路程都是甲的二倍,B选项错误;
=40千米/时,乙的速度是甲的速度的2倍,所以在乙到达终点之前,乙行驶的路程都是甲的二倍,B选项错误;
乙到达终点时所需时间为![]() =3(小时),3小时甲行驶3×20=60(千米),离终点还有120-60=60(千米),故C选项正确,
=3(小时),3小时甲行驶3×20=60(千米),离终点还有120-60=60(千米),故C选项正确,
当0<t≤2时,S=-60t+120,当S=90时,即-60t+120=90,解得:t=0.5,
当3<t≤6时,S=20t,当S=90时,即20t=90,解得:t=4.5,
∴若两人相距90千米,则t=0.5或t=4.5,故D正确.
故选B.


科目:初中数学 来源: 题型:
【题目】用直尺和圆规画一个角等于已知角,是运用了“全等三角形的对应角相等”这一性质,其全等的依据是( )

A.SAS B.ASA C.AAS D.SSS
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,直角边为a、b,斜边为c.若把关于x的方程ax2+![]() cx+b=0称为“勾系一元二次方程”,则这类“勾系一元二次方程”的根的情况是( )
cx+b=0称为“勾系一元二次方程”,则这类“勾系一元二次方程”的根的情况是( )
A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 没有实数根 D. 一定有实数根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级(1)班张山同学利用所学函数知识,对函数y=|x+2|﹣x﹣1进行了如下研究:
列表如下:
x | ﹣5 | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | ||
Y | 7 | 5 | 3 | m | 1 | n | 1 | 1 | 1 |
描点并连线(如下图)
(1)求表格中的m、n的值;
(2)在给出的坐标系中画出函数y=|x+2|﹣x﹣1的图象;
(3)一次函数y=﹣x+3的图象与函数y=|x+2|﹣x﹣1的图象交点的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年北疆承办了世界园艺博览会,某商店为了抓住博览会的商机,决定购买A.B两种世园会纪念品,若购进A中纪念品20件,B种纪念品10件,需要2000元;若购进A中纪念品8件,B种纪念品6件,需要1100元.
(1)求购进A.B两种纪念品每件各需要多少元?
(2)若该商店决定拿出10000元全部用来购进这两种纪念品,考虑到市场需求,要求购进A种纪念品的数量不少于B种的6倍,且少于B种纪念品数量的8倍,设购进B种纪念品a件,则该商店共有几种进货方案?
(3)在第(2)问的条件下,若销售每件A种纪念品可获利润30元,每件B种纪念品可获利润40元,设总利润为y元,请写出总利润y(元)与a(个)的函数关系式,并根据函数关系式说明总利润最高时的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一座抛物线形拱桥,正常水位时桥下水面宽度为20m,拱顶距离水面4m.
(1)在如图所示的直角坐标系中,求出该抛物线的解析式.
(2)在正常水位的基础上,当水位上升h(m)时,桥 下水面的宽度为d(m),试求出用d表示h的函数关系式;
(3)设正常水位时桥下的水深为2m,为保证过往船只顺利航行,桥下水面的宽度不得小于18m,求
水深超过多少米时就会影响过往船只在桥下顺利航行?

查看答案和解析>>
科目:初中数学 来源: 题型:
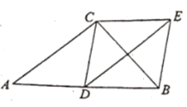
【题目】如图,已知在Rt△ABC 中,∠ACB=90°,D 是边 AB 上的中点,DE 平分∠CDB,且 DE=AC.
(1)求证:CE=AD;
(2)如果AC=BC,求证:四边形BECD 是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
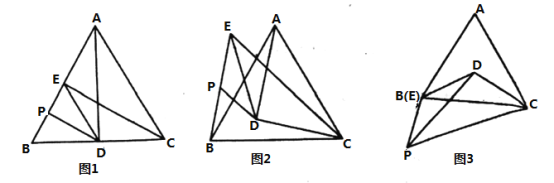
【题目】已知等边![]() 和等腰
和等腰![]() ,
,![]() ,
,![]() .
.
(1)如图1,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,
上,![]() 是
是![]() 的中点,连接
的中点,连接![]() ,
,![]() ,则线段
,则线段![]() 与
与![]() 之间的数量关系为 ;
之间的数量关系为 ;
(2)如图2,点![]() 在
在![]() 内部,点
内部,点![]() 在
在![]() 外部,
外部,![]() 是
是![]() 的中点,连接
的中点,连接![]() ,
,![]() ,则(1)中的结论是否仍然成立?若成立,请给出证明,若不成立,请说明理由.
,则(1)中的结论是否仍然成立?若成立,请给出证明,若不成立,请说明理由.
(3)如图3,若点![]() 在
在![]() 内部,点
内部,点![]() 和点
和点![]() 重合,点
重合,点![]() 在
在![]() 下方,且
下方,且![]() 为定值,当
为定值,当![]() 最大时,
最大时,![]() 的度数为 .
的度数为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com