
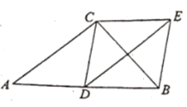
【题目】如图,已知在Rt△ABC 中,∠ACB=90°,D 是边 AB 上的中点,DE 平分∠CDB,且 DE=AC.
(1)求证:CE=AD;
(2)如果AC=BC,求证:四边形BECD 是正方形.
【答案】(1)详见解析;(2)详见解析
【解析】
(1)先证明AC∥DE,再由一组对边平行且相等即可证明四边形ACED是平行四边形,从而证明CE=AD;
(2)先证明四边形CDBE是菱形,再由等腰三角形三线合一的性质证明CD⊥BD,从而证明四边形BECD 是正方形.
(1)证明:∵∠ACB=90°,D 是边 AB 上的中点,
∴CD=AD=BD
∴∠ACD=∠A,
∴∠CDB=∠ACD+∠A=2∠A,
∵DE平分∠CDB
∴∠BDE=![]() ,
,
∴∠A=∠BDE,
∴AC∥DE,
又∵DE=AC,
∴四边形ACED是平行四边形,
∴CE=AD
(2)证明:由(1)可得,四边形ACED是平行四边形,
∴CE∥AD,CE=AD,
∵AD=BD=CD
∴CE=BD=CD
∴四边形CDBE是菱形,
又∵AC=BC,点D是AB中点,
∴CD⊥BD
∴菱形CDBE是正方形.


科目:初中数学 来源: 题型:
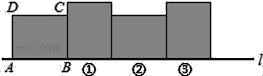
【题目】如图,在矩形ABCD中,已知AB=4,BC=3,矩形在直线上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续向右旋转90°至图②位置,…,以此类推,这样连续旋转2015次后,顶点A在整个旋转过程中所经过的路程之和是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A,B两地相距120千米,甲乙两人沿同一条公路匀速行驶,甲骑自行车以20千米/时从A地前往B地,同时乙骑摩托车从B地前往A地,设两人之间的距离为s(千米),甲行驶的时间为t(小时),若s与t的函数关系如图所示,则下列说法错误的是( )
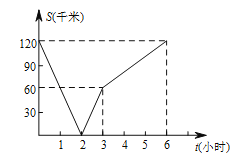
A.经过2小时两人相遇
B.若乙行驶的路程是甲的2倍,则t=3
C.当乙到达终点时,甲离终点还有60千米
D.若两人相距90千米,则t=0.5或t=4.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场以每件280元的价格购进一批商品,当每件商品售价为360元时,每月可售出60件,为了扩大销售,商场决定采取适当降价的方式促销,经调查发现,如果每件商品降价1元,那么商场每月就可以多售出5件.
(1)设商场每件商品降价x元,利润为y元,写出y与x的函数关系式。
(2)当该商品的销售价为多少元时,所获利润最大?最大利润是多少?
(3)要使商场每月销售这种商品的利润达到7200元,且更有利于减少库存,则每件商品应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
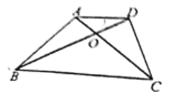
【题目】如图,已知梯形 ABCD 中,AD∥BC,对角线 AC、BD 相交于点O, △AOB 与△BOC 的面积分别为 4、8,则梯形ABCD 的面积等于___________
查看答案和解析>>
科目:初中数学 来源: 题型:
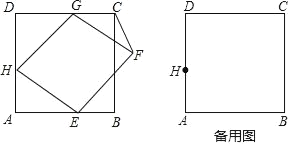
【题目】如图,已知正方形ABCD的边长为3,菱形EFGH的三个顶点E、G、H分别在正方形的边AB、CD、DA上,AH=1,联结CF.
(1)当DG=1时,求证:菱形EFGH为正方形;
(2)设DG=x,△FCG的面积为y,写出y关于x的函数解析式,并指出x的取值范围;
(3)当DG=![]() 时,求∠GHE的度数.
时,求∠GHE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“一带一路”战略的影响下,某茶叶经销商准备把“茶路”融入“丝路”,经计算,他销售10斤A级别和20斤B级别茶叶的利润为4000元,销售20斤A级别和10斤B级别茶叶的利润为3500元
(1)分别求出每斤A级别茶叶和每斤B级别茶叶的销售利润;
(2)若该经销商一次购进两种级别的茶叶共200斤用于出口.设购买A级别茶叶a斤(70≤a≤120),销售完A、B两种级别茶叶后获利w元.
①求出w与a之间的函数关系式;
②该经销商购进A、B两种级别茶叶各多少斤时,才能获取最大的利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“作圆的内接正方形”的尺规作图过程。
已知:⊙O.
求作:圆的内接正方形.
如图,
(1)过圆心O作直线AC,与⊙O相交于A,C两点;
(2)过点O作直线BD⊥AC,交⊙O于B,D两点;
(3)连接AB,BC,CD,DA。
∴四边形ABCD为所求。

请回答:该尺规作图的依据是____________________________。(写出两条)
查看答案和解析>>
科目:初中数学 来源: 题型:
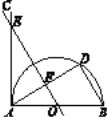
【题目】已知:如图, ![]() 是半圆
是半圆![]() 的直径,D是半圆上的一个动点(点D不与点A,B 重合),
的直径,D是半圆上的一个动点(点D不与点A,B 重合), ![]()
(1)求证:AC是半圆![]() 的切线;
的切线;

(2)过点O作BD的平行线,交AC于点E,交AD于点F,且EF=4, AD=6, 求BD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com