【题目】下面是“作圆的内接正方形”的尺规作图过程。
已知：⊙O.
求作：圆的内接正方形.
如图，
（1）过圆心O作直线AC,与⊙O相交于A,C两点；
（2）过点O作直线BD⊥AC,交⊙O于B,D两点；
（3）连接AB,BC,CD,DA。
∴四边形ABCD为所求。
请回答：该尺规作图的依据是____________________________。（写出两条）
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
【题目】在Rt△ABC中，直角边为a、b，斜边为c．若把关于x的方程ax2+
cx+b=0称为“勾系一元二次方程”，则这类“勾系一元二次方程”的根的情况是（ ）
A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 没有实数根 D. 一定有实数根
查看答案和解析>>
科目：初中数学 来源： 题型：
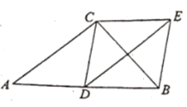
【题目】如图，已知在Rt△ABC 中，∠ACB=90°，D 是边 AB 上的中点，DE 平分∠CDB，且 DE=AC．
（1）求证：CE=AD；
（2）如果AC=BC，求证：四边形BECD 是正方形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在
中，按以下步骤作图：
第一步：分别以点
为圆心，以大于
的长为半径画弧，两弧相交于
两点；
第二步：作直线
交
于点
，连接
．
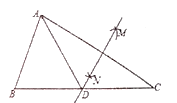
（1）
是______三角形；(填“等边”、“直角”、“等腰”)
（2）若
，则
的度数为___________．
查看答案和解析>>
科目：初中数学 来源： 题型：
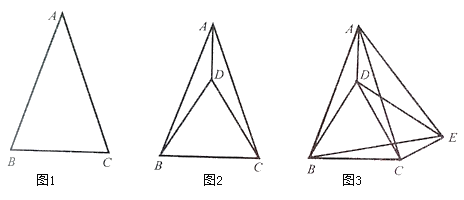
【题目】如图1，张老师在黑板上画出了一个
，其中
，让同学们进行探究．
（1）探究一：
如图2，小明以
为边在内部作等边
，连接
，请直接写出
的度数_____________；
（2）探究二：
如图3，小彬在（1）的条件下，又以
为边作等边
，连接
.判断与的数量关系；并说明理由；
（3）探究三：
如图3，小聪在（2）的条件下，连接
，若
，求
的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
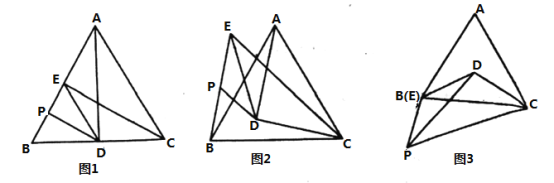
【题目】已知等边
和等腰
，
，
．
（1）如图1，点
在
上，点
在
上，
是
的中点，连接
，
，则线段与之间的数量关系为 ；
（2）如图2，点在内部，点在外部，是的中点，连接，，则（1）中的结论是否仍然成立？若成立，请给出证明，若不成立，请说明理由．
（3）如图3，若点在内部，点和点
重合，点
在下方，且
为定值，当最大时，
的度数为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在等腰Rt△ABC中，∠ACB=90°，D为BC的中点，DE⊥AB，垂足为E，过点B作BF∥AC交DE的延长线于点F，连接CF．
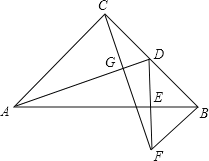
（1）求证：CD=BF；
（2）求证：AD⊥CF；
（3）连接AF，试判断△ACF的形状．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
