
【题目】如图1,张老师在黑板上画出了一个![]() ,其中
,其中![]() ,让同学们进行探究.
,让同学们进行探究.
(1)探究一:
如图2,小明以![]() 为边在
为边在![]() 内部作等边
内部作等边![]() ,连接
,连接![]() ,请直接写出
,请直接写出![]() 的度数_____________;
的度数_____________;
(2)探究二:
如图3,小彬在(1)的条件下,又以![]() 为边作等边
为边作等边![]() ,连接
,连接![]() .判断
.判断![]() 与
与![]() 的数量关系;并说明理由;
的数量关系;并说明理由;
(3)探究三:
如图3,小聪在(2)的条件下,连接![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
【答案】(1)150;(2)CE=AD.理由见解析;(3)![]() .
.
【解析】
(1)根据已知条件可知△ABD≌△ACD,进而得出∠ADB的度数;
(2)通过证明△ABD≌△EBC即可解答;
(3)通过前两问得出∠DCE=90°,通过角度运算得出∠BDE=90°,分别由勾股定理运算即可得.
(1)∵△BCD是等边三角形,
∴BD=BC,∠BDC=60°
∴在△ABD与△ACD中,
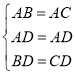
∴△ABD≌△ACD(SSS),
∴∠ADB=∠ADC=![]()
故答案为:150°
(2)结论:CE=AD.
理由:∵△BDC、△ABE都是等边三角形,
∴∠ABE=∠DBC=60°,AB=BE,BD=DC,
∴∠ABE﹣∠DBE=∠DBC﹣∠DBE,
∴∠ABD=∠EBC,
在△ABD和△EBC中
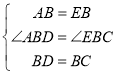 ,
,
∴△ABD≌△EBC(SAS)
∴CE=AD
(3)∵△ABD≌△EBC,
∴∠BDA=∠ECB=150°
∵∠BCD=60°,
∴∠DCE=90°.
∵∠DEC=60°,
∴∠CDE=30°
∵DE=2,
∴CE=1,
由勾股定理得:DC=BC=![]() ,
,
∵∠BDE=60°+30°=90°,DE=2,BD=![]()
由勾股定理得:BE=![]()
∵△ABE是等边三角形,
∴AE=BE=![]() .
.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】已知等腰三角形ABC的底边BC=20cm,D是腰AB上一点,且CD=16cm,BD=12cm
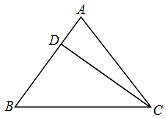
(1)请判断CD与AB的位置关系,并说明理由;
(2)求该三角形的腰的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
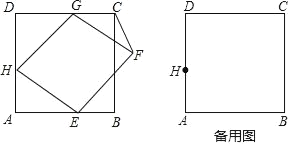
【题目】如图,已知正方形ABCD的边长为3,菱形EFGH的三个顶点E、G、H分别在正方形的边AB、CD、DA上,AH=1,联结CF.
(1)当DG=1时,求证:菱形EFGH为正方形;
(2)设DG=x,△FCG的面积为y,写出y关于x的函数解析式,并指出x的取值范围;
(3)当DG=![]() 时,求∠GHE的度数.
时,求∠GHE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
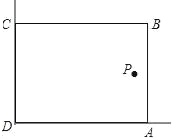
【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),则花园面积S的最大值为_____m2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“作圆的内接正方形”的尺规作图过程。
已知:⊙O.
求作:圆的内接正方形.
如图,
(1)过圆心O作直线AC,与⊙O相交于A,C两点;
(2)过点O作直线BD⊥AC,交⊙O于B,D两点;
(3)连接AB,BC,CD,DA。
∴四边形ABCD为所求。

请回答:该尺规作图的依据是____________________________。(写出两条)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】涟水外卖市场竞争激烈,美团、饿了么等公司订单大量增加,某公司负责招聘外卖送餐员,具体方案如下:每月不超出750单,每单收入4元;超出750单的部分每单收入m元.
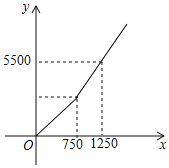
(1)若某“外卖小哥”某月送了500单,收入 元;
(2)若“外卖小哥”每月收入为y(元),每月送单量为x单,y与x之间的关系如图所示,求y与x之间的函数关系式;
(3)若“外卖小哥”甲和乙在某个月内共送单1200单,且甲送单量低于乙送单量,共收入5000元,问:甲、乙送单量各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
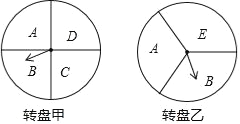
【题目】某超市在端午节期间开展优惠活动,凡购物者可以通过转动转盘的方式享受折扣优惠,本次活动共有两种方式,方式一:转动转盘甲,指针指向 A区域时,所购买物品享受9折优惠、指针指向其它区域无优惠;方式二: 同时转动转盘甲和转盘乙,若两个转盘的指针指向每个区域的字母相同,所购买物品享受8折优惠,其它情况无优惠.在每个转盘中,指针指向每个区城的可能性相同(若指针指向分界线,则重新转动转盘)
(1)若顾客选择方式一,则享受 9 折优惠的概率为_______;
(2)若顾客选择方式二,请用树状图或列表法列出所有可能,并求顾客享受8折优惠的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com