
【题目】在△![]() 和△
和△![]() 中,
中,![]() ,
,![]() 和
和![]() 分别为
分别为![]() 边和
边和![]() 边上的中线,再从以下三个条件:①
边上的中线,再从以下三个条件:①![]() ;②
;②![]() ;③
;③![]() 中任取两个为已知条件,另一个为结论,则最多可以构成_______个正确的命题.
中任取两个为已知条件,另一个为结论,则最多可以构成_______个正确的命题.
【答案】1
【解析】
分别讨论如果①②,那么③;如果①③,那么②;如果②③,那么①三种情况,根据全等三角形的判定定理逐一判断即可的答案.
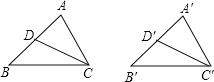
如图,当![]() ,
,![]() 时,
时,
∵![]() 和
和![]() 分别为
分别为![]() 边和
边和![]() 边上的中线,
边上的中线,
∴AD=A′D′,
在△ADC和△A′D′C′中,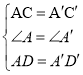 ,
,
∴△ADC≌△A′D′C′,(SAS)
∴CD=C′D′,
∴如果①②,那么③是真命题,
当![]() ,
,![]() ,
,
同理可得:AD=A′D′,
∵SSA不能判定△ADC≌△A′D′C′,
∴不能判定AC=A′C′,故如果①③,那么②不是真命题,
当![]() ,
,![]() 时,
时,
∵SSA不能判定△ADC≌△A′D′C′,
∴不能判定AD=A′D′,
∴不能判定AB=A′B′,故如果②③,那么①不是真命题,
综上所述:是真命题的有1种,
故答案为:1


科目:初中数学 来源: 题型:
【题目】有一座抛物线形拱桥,正常水位时桥下水面宽度为20m,拱顶距离水面4m.
(1)在如图所示的直角坐标系中,求出该抛物线的解析式.
(2)在正常水位的基础上,当水位上升h(m)时,桥 下水面的宽度为d(m),试求出用d表示h的函数关系式;
(3)设正常水位时桥下的水深为2m,为保证过往船只顺利航行,桥下水面的宽度不得小于18m,求
水深超过多少米时就会影响过往船只在桥下顺利航行?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,按以下步骤作图:
中,按以下步骤作图:
第一步:分别以点![]() 为圆心,以大于
为圆心,以大于![]() 的长为半径画弧,两弧相交于
的长为半径画弧,两弧相交于![]() 两点;
两点;
第二步:作直线![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
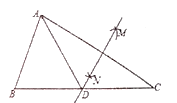
(1)![]() 是______三角形;(填“等边”、“直角”、“等腰”)
是______三角形;(填“等边”、“直角”、“等腰”)
(2)若![]() ,则
,则![]() 的度数为___________.
的度数为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边![]() 和等腰
和等腰![]() ,
,![]() ,
,![]() .
.
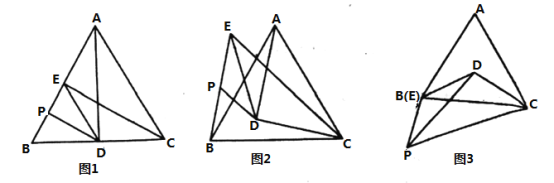
(1)如图1,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,
上,![]() 是
是![]() 的中点,连接
的中点,连接![]() ,
,![]() ,则线段
,则线段![]() 与
与![]() 之间的数量关系为 ;
之间的数量关系为 ;
(2)如图2,点![]() 在
在![]() 内部,点
内部,点![]() 在
在![]() 外部,
外部,![]() 是
是![]() 的中点,连接
的中点,连接![]() ,
,![]() ,则(1)中的结论是否仍然成立?若成立,请给出证明,若不成立,请说明理由.
,则(1)中的结论是否仍然成立?若成立,请给出证明,若不成立,请说明理由.
(3)如图3,若点![]() 在
在![]() 内部,点
内部,点![]() 和点
和点![]() 重合,点
重合,点![]() 在
在![]() 下方,且
下方,且![]() 为定值,当
为定值,当![]() 最大时,
最大时,![]() 的度数为 .
的度数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC的三边AB,BC,CA分别拉长到原来的两倍,得点D,E,F,已知△DEF的面积为42,则△ABC的面积为( )
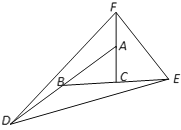
A.14B.7C.6D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,∠ACB=90°,D为BC的中点,DE⊥AB,垂足为E,过点B作BF∥AC交DE的延长线于点F,连接CF.
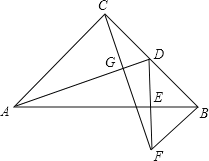
(1)求证:CD=BF;
(2)求证:AD⊥CF;
(3)连接AF,试判断△ACF的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图显示了用计算机模拟随机抛掷一枚硬币的某次实验的结果
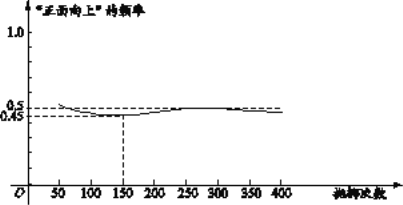
下面有三个推断:
①当抛掷次数是100时,计算机记录“正面向上”的次数是47,所以“正面向上”的概率是0.47;
②随着试验次数的增加,“正面向上”的频率总在0.5附近摆动,显示出一定的稳定性,可以估计“正面向上”的概率是0.5;
③若再次用计算机模拟此实验,则当抛掷次数为150时,“正面向上”的频率一定是0.45.
其中合理的是
A. ① B. ② C. ①② D. ①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】判断题,正确的打“√”,错误的打“×”.
(1)![]() ,得
,得![]() (______). (2)由
(______). (2)由![]() ,得
,得![]() (______).
(______).
(3)2是不等式![]() 的解(______). (4)由
的解(______). (4)由![]() ,得
,得![]() (______).
(______).
(5)如果![]() ,
,![]() ,则
,则![]() (______). (6)如果
(______). (6)如果![]() ,则
,则![]() (______).
(______).
(7)![]() (______)
(______)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com