
【题目】判断题,正确的打“√”,错误的打“×”.
(1)![]() ,得
,得![]() (______). (2)由
(______). (2)由![]() ,得
,得![]() (______).
(______).
(3)2是不等式![]() 的解(______). (4)由
的解(______). (4)由![]() ,得
,得![]() (______).
(______).
(5)如果![]() ,
,![]() ,则
,则![]() (______). (6)如果
(______). (6)如果![]() ,则
,则![]() (______).
(______).
(7)![]() (______)
(______)
 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
【题目】在“一带一路”战略的影响下,某茶叶经销商准备把“茶路”融入“丝路”,经计算,他销售10斤A级别和20斤B级别茶叶的利润为4000元,销售20斤A级别和10斤B级别茶叶的利润为3500元
(1)分别求出每斤A级别茶叶和每斤B级别茶叶的销售利润;
(2)若该经销商一次购进两种级别的茶叶共200斤用于出口.设购买A级别茶叶a斤(70≤a≤120),销售完A、B两种级别茶叶后获利w元.
①求出w与a之间的函数关系式;
②该经销商购进A、B两种级别茶叶各多少斤时,才能获取最大的利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△![]() 和△
和△![]() 中,
中,![]() ,
,![]() 和
和![]() 分别为
分别为![]() 边和
边和![]() 边上的中线,再从以下三个条件:①
边上的中线,再从以下三个条件:①![]() ;②
;②![]() ;③
;③![]() 中任取两个为已知条件,另一个为结论,则最多可以构成_______个正确的命题.
中任取两个为已知条件,另一个为结论,则最多可以构成_______个正确的命题.
查看答案和解析>>
科目:初中数学 来源: 题型:
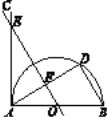
【题目】已知:如图, ![]() 是半圆
是半圆![]() 的直径,D是半圆上的一个动点(点D不与点A,B 重合),
的直径,D是半圆上的一个动点(点D不与点A,B 重合), ![]()
(1)求证:AC是半圆![]() 的切线;
的切线;

(2)过点O作BD的平行线,交AC于点E,交AD于点F,且EF=4, AD=6, 求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年,在新泰市美丽乡村建设中,甲、乙两个工程队分别承担某处村级道路硬化和道路拓宽改造工程.己知道路硬化和道路拓宽改造工程的总里程数是8.6千米,其中道路硬化的里程数是道路拓宽里程数的2倍少1千米.
(1)求道路硬化和道路拓宽里程数分别是多少千米;
(2)甲、乙两个工程队同时开始施工,甲工程队比乙工程队平均每天多施工10米.由于工期需要,甲工程队在完成所承担的![]() 施工任务后,通过技术改进使工作效率比原来提高了
施工任务后,通过技术改进使工作效率比原来提高了![]() .设乙工程队平均每天施工
.设乙工程队平均每天施工![]() 米,若甲、乙两队同时完成施工任务,求乙工程队平均每天施工的米数
米,若甲、乙两队同时完成施工任务,求乙工程队平均每天施工的米数![]() 和施工的天数.
和施工的天数.
查看答案和解析>>
科目:初中数学 来源: 题型:
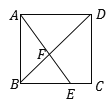
【题目】如图所示,在正方形ABCD中,点E是BC边上一点,且BE:EC=2:1,AE与BD交于点F,则△AFD与四边形DFEC的面积之比是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M,N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A,B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,设移动时间为t(单位:秒,0<t<2.5).

(1)当t为何值时,以A,P,M为顶点的三角形与△ABC相似?
(2)是否存在某一时刻t,使四边形APNC的面积S有最小值?若存在,求S的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.填空:
①∠AEB的度数为______;
②线段AD,BE之间的数量关系为______.
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①![]() ;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )

A. ①②③④ B. ①④ C. ②③④ D. ①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com