
����Ŀ����ͼ�������� ![]() ��ֱ��
��ֱ�� ![]() ����A��B���㣬��A��x���ϣ���B�ĺ�������2����P��ֱ��AB�Ϸ����������ϣ�����P�ֱ���PC��y�ᡢPD��x�ᣬ��ֱ��AB���ڵ�C��D����PC��PDΪ��������PCQD�����Q������Ϊ��m��n����
����A��B���㣬��A��x���ϣ���B�ĺ�������2����P��ֱ��AB�Ϸ����������ϣ�����P�ֱ���PC��y�ᡢPD��x�ᣬ��ֱ��AB���ڵ�C��D����PC��PDΪ��������PCQD�����Q������Ϊ��m��n����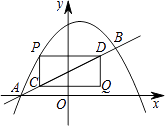
��1����A�������� �� ��B����������
��2������������������Ӧ�ĺ�����ϵʽ��
��3����m��n֮��ĺ�����ϵʽ����Ҫ��д���Ա���n��ȡֵ��Χ����
��4����ֱ��д������PCQD���ܳ����ʱn��ֵ��
���𰸡�
��1������2��0������2��2��
��2��
�⣺�����⣬�� 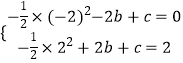 ��
��
��� ![]()
���ԣ���������������Ӧ�ĺ�����ϵʽΪy=�� ![]() x2+
x2+ ![]() x+3��
x+3��
��3��
�⣺�ߵ�Q������Ϊ��m��n����
�� ![]() x+1=n��
x+1=n��
���x=2n��2��
���ԣ���C������Ϊ��2n��2��n����
��D��������m�� ![]() m+1����
m+1����
���P��������2n��2�� ![]() m+1����
m+1����
����2n��2�� ![]() m+1������y=��
m+1������y=�� ![]() x2+
x2+ ![]() x+3���é�
x+3���é� ![]() ����2n��2��2+
����2n��2��2+ ![]() ����2n��2��+3=
����2n��2��+3= ![]() m+1��
m+1��
�����ã�m=��4n2+10n��2��
���ԣ�m��n֮��ĺ�����ϵʽ��m=��4n2+10n��2��
��4��
�⣺��C��2n��2��n����P��2n��2�� ![]() m+1����Q��m��n����
m+1����Q��m��n����
��PC= ![]() m+1��n��CQ=m����2n��2��=m��2n+2��
m+1��n��CQ=m����2n��2��=m��2n+2��
�����PCQD���ܳ�=2�� ![]() m+1��n+m��2n+2����
m+1��n+m��2n+2����
=3m��6n+6��
=3����4n2+10n��2����6n+6��
=��12n2+24n��
=��12��n��1��2+12��
�൱n=1ʱ������PCQD���ܳ����
���������⣺��1����y=0���� ![]() x+1=0��
x+1=0��
���x=��2��
���ԣ���A����2��0����
�ߵ�B�ĺ�������2��
��y= ![]() ��2+1=2��
��2+1=2��
��B��2��2����
�����㾫�������ö��κ�����ͼ��Ͷ��κ��������ʶ���Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪���κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣻�����ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ഺ��֧���ھ���ƶ��У���������ƶ����ͥ���ͼס������������������֣���֪��������ļ۸�ȼ��������10Ԫ����480Ԫ������������Ŀ���ǡ������360Ԫ�����������Ŀ�����ͬ��
��1����ס�����������ÿ�õļ۸���Ƕ���Ԫ��
��2����ʵ�ʰ���У����Ǿ����ٴι���ס����������繲50�ã���ʱ������������ۼ۱ȵ�һ�ι���ʱ������10%������������ۼ۲��䣬����ٴι�������������ܷ��ò�����1500Ԫ����ô�������ɹ�����ٿ��������磿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֱ����ABC�У���BAC=90![]() ��AD��BC��D����ABC��ƽ���߷ֱ�AC��AD��E��F���㣬MΪEF���е㣬�ӳ�AM��BC�ڵ�N������DM�����н��ۣ���AE=AF����AM��EF����AF=DF����DF=DN��������ȷ�Ľ����У�������
��AD��BC��D����ABC��ƽ���߷ֱ�AC��AD��E��F���㣬MΪEF���е㣬�ӳ�AM��BC�ڵ�N������DM�����н��ۣ���AE=AF����AM��EF����AF=DF����DF=DN��������ȷ�Ľ����У�������

A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ���k2x2��2��k+1��x+1=0������ʵ������
��1����k��ȡֵ��Χ��
��2����k=1ʱ�����������̵��������ֱ�Ϊx1��x2 �� �� ![]() +
+ ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����ABC�ڽ��ڡ�O����D��OC���ӳ����ϣ�sinB= ![]() ����CAD=30�㣮
����CAD=30�㣮
��1����֤��AD�ǡ�O�����ߣ�
��2����OD��AB��BC=5����AD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD���ŶԽ���BD�۵���ʹ��C����![]() ����
����![]() ��AD�ڵ�E��
��AD�ڵ�E��
��1�����жϡ�BDE����״����˵�����ɣ�
��2����![]() ��
��![]() �����BDE�������
�����BDE�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijҽҩ�о���������һ����ҩ��������ҩЧʱ���֣�������˰��涨�������ã���ô��ҩ��2СʱʱѪҺ�к�ҩ����ߣ���ÿ����8�ˣ�1000��=1���ˣ���������˥����10СʱʱѪҺ�к�ҩ��Ϊÿ����4�ˣ�ÿ����ѪҺ�к�ҩ��y���ˣ�����ʱ��x��Сʱ���ı仯��ͼ��ʾ�������˰��涨������ҩ��
��1����y��x֮��Ľ���ʽ��
��2�����ÿ����ѪҺ�к�ҩ��������3�˻�3������ʱ�������Ƽ���ʱ����Ч�ģ���ô�����Чʱ���Ƕ���Сʱ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ������E��������ABCD��BC���ϣ�BF��AE�ڵ�F��DG��AE�ڵ�G����֪��ADG�ա�BAF.����Ҫ��֤����

��չ����ͼ������B��C����MAN�ı�AM��AN�ϣ���E, F����MAN�ڲ�������AD�ϣ���1����2�ֱ�����ABE����CAF����ǣ���֪AB=AC,��1=��2=��BAC.��֤����ABE�ա�CAF.
Ӧ�ã���ͼ�����ڵ���������ABC�У�AB=AC��AB��BC����D�ڱ�B�ϣ�CD=2BD.��E, F���߶�AD�ϣ���1=��2=��BAC������ABC�����Ϊ9������ABE����CDF�����֮��Ϊ_________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2015��4��30�գ������⽭����ȫ��������ϣ����Ʒ��Ų���6460�ţ�ÿ���ϵIJ�����200�����ң����漰6�������漴��ʼ�������֣�С������¼�IJ��ַ�����������ʾ������Թ��Ʋ��ַ����ɹ��ĸ���Ϊ�� ��
�ۼƲ��ַ�������/�� | 200 | 400 | 600 | 800 | 1000 | 1200 | 1400 |
�����ɹ���/�� | 181 | 362 | 541 | 718 | 905 | 1077 | 1263 |
A.0.95
B.0.9
C.0.85
D.0.8
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com