
����Ŀ����֪����ͼ������E��������ABCD��BC���ϣ�BF��AE�ڵ�F��DG��AE�ڵ�G����֪��ADG�ա�BAF.����Ҫ��֤����

��չ����ͼ������B��C����MAN�ı�AM��AN�ϣ���E, F����MAN�ڲ�������AD�ϣ���1����2�ֱ�����ABE����CAF����ǣ���֪AB=AC,��1=��2=��BAC.��֤����ABE�ա�CAF.
Ӧ�ã���ͼ�����ڵ���������ABC�У�AB=AC��AB��BC����D�ڱ�B�ϣ�CD=2BD.��E, F���߶�AD�ϣ���1=��2=��BAC������ABC�����Ϊ9������ABE����CDF�����֮��Ϊ_________.
���𰸡���չ��֤����������Ӧ�ã�6
��������
��չ��֤������ͼ��
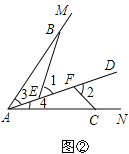
�ߡ�1=��2�����BEA=��AFC��
�ߡ�1=��ABE+��3����3+��4=��BAC����1=��BAC��
���BAC=��ABE+��3�����4=��ABE��
�ߡ�AEB=��AFC����ABE=��4��AB=AC��
���ABE�ա�CAF��AAS����
Ӧ�ã�6��
��չ��������1=��2=��BAC������������������ʵó���4=��ABE���Ӷ�����AAS֤����ABE�ա�CAF��
Ӧ�ã����ȸ�����ABD����ADC�ȸߣ��ױ߱�ֵΪ��1��2���ó���ABD����ADC�����Ϊ��1��2����֤����ABE�ա�CAF�����ɵó���ABE����CDF�����֮��Ϊ��ADC������ó��𰸼��ɣ�
��ͼ��
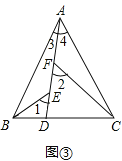
���ڵ���������ABC�У�AB=AC��CD=2BD��
���ABD����ADC�ȸߣ��ױ߱�ֵΪ��1��2��
���ABD����ADC�������1��2��
�ߡ�ABC�����Ϊ9�����ABD����ADC����ֱ�Ϊ��3��6��
�ߡ�1=��2�����BEA=��AFC��
�ߡ�1=��ABE+��3����3+��4=��BAC����1=��BAC��
���BAC=��ABE+��3�����4=��ABE��
�ߡ�AEB=��AFC����ABE=��4��AB=AC�����ABE�ա�CAF��AAS����
���ABE����CAF�����ȣ����ABE����CDF�����֮��Ϊ��ADC�������
���ABE����CDF�����֮��Ϊ6��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��BD�ǡ�ABC��ƽ���ߣ�DE��CB����AB�ڵ�E����A��45�㣬��BDC��60��.����BDE���ڽǵĶ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������� ![]() ��ֱ��
��ֱ�� ![]() ����A��B���㣬��A��x���ϣ���B�ĺ�������2����P��ֱ��AB�Ϸ����������ϣ�����P�ֱ���PC��y�ᡢPD��x�ᣬ��ֱ��AB���ڵ�C��D����PC��PDΪ��������PCQD�����Q������Ϊ��m��n����
����A��B���㣬��A��x���ϣ���B�ĺ�������2����P��ֱ��AB�Ϸ����������ϣ�����P�ֱ���PC��y�ᡢPD��x�ᣬ��ֱ��AB���ڵ�C��D����PC��PDΪ��������PCQD�����Q������Ϊ��m��n����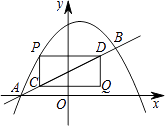
��1����A�������� �� ��B����������
��2������������������Ӧ�ĺ�����ϵʽ��
��3����m��n֮��ĺ�����ϵʽ����Ҫ��д���Ա���n��ȡֵ��Χ����
��4����ֱ��д������PCQD���ܳ����ʱn��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̫ԭ�й������г��Ľ����ٶȡ�����������������ָ���Ⱦ�ȫ����λ���������г����Ľ���ʾ��ͼ��ͼ��ʾ��AB��AD��AD��DC����B��C��EF�ϣ�EF��HG��EH��HG��AB=75cm��AD=24cm��BC=25cm��EH=4cm�����A������ľ����� cm��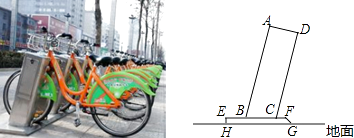
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��PA����O��A��B���㣬AE�ǡ�O��ֱ������CΪ��O��һ�㣬��ACƽ�֡�PAE����C��CD��PA������ΪD��
��1����֤��CDΪ��O�����ߣ�
��2����CD=2AD����O��ֱ��Ϊ20�����߶�AC��AB�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=x��4��x�ᡢy��ֱ���M��N���㣬��O�İ뾶Ϊ2������O��ÿ��1����λ���ٶ�������ƽ���˶������ƶ�ʱ����ʱ��ֱ��MNǡ����Բ���У� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ������ȫ�ȵĵȱ������εı߳�Ϊ1m��һ���ͻ�������A�㿪ʼ��ABCDBEA��˳���صȱ������εı�ѭ���˶�������2012mͣ�£�������ͻ�����ͣ�ڣ� ��

A����A�� B����B�� C����C�� D����E��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУΪ����ǿѧ�����ʣ�����������������������Ŀ��A����Bƹ����C������D����ӣ�Ϊ�˽�ѧ����ϲ����һ�ֻ��Ŀ�������ȡ�˲���ѧ�����е��飬�������������Ƴ���������������ͳ��ͼ����ش��������⣺
��1����α������ѧ�������ˣ�
��2�����㽫����ͳ��ͼ������ɣ�
��3����ƽʱ��ƹ������Ŀѵ���У��ס��ҡ����������˱������㣬�־�����������ͬѧ����ѡ�����μ�ƹ�����������ǡ��ѡ�мס�����λͬѧ�ĸ��ʣ�����״ͼ���б�����𣩣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�DΪAC����һ�㣬��DBC=��A��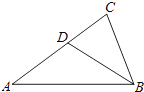
��1����֤����BCD�ס�ACB��
��2�����BC= ![]() ��AC=3����CD�ij���
��AC=3����CD�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com