
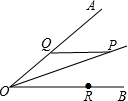
 如图所示,∠AOB=30°,角内有点P,PO=10cm,两边上各有一点Q,R(均不同于点O),则△PQR的周长最小值是10.
如图所示,∠AOB=30°,角内有点P,PO=10cm,两边上各有一点Q,R(均不同于点O),则△PQR的周长最小值是10. 分析 设点P关于OA的对称点是E,关于OB的对称点是F,当点R、Q在EF上时,△PQR的周长=PQ+QR+PR=EF,此时周长最小.
解答 解:如图,
作出点P关于OA的对称点E,作出点P关于OB的对称点F,连接EF,交OA于Q,交OB于R.连接PQ,PR,PE,PF,OE,OF.
则PQ=EQ,PR=RF,
则△PQR的周长=PQ+QR+PR=EQ+QR+RF=EF.
∵∠AOP=∠AOE,∠POB=∠FOB,∠AOB=∠AOP+∠POB=30°,
∴∠EOF=60°,
又∵OE=OP,OF=OP,
∴OE=OF=10,
即△EOF是等边三角形,
∴EF=OP=10,
所以△PQR的周长的最小值为10.
故答案为:10.
点评 此题考查最短路径问题,关键是根据等腰直角三角形的判定和性质,轴对称的性质等知识进行分析.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
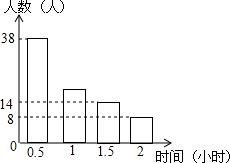 随着“微信”的流行,不少初中学生在微信朋友圈忙着“发状态”,某校在使用微信的学生中随机抽取了部分,并调查他们平常每天上微信的时间,绘制了统计表和条形统计图:
随着“微信”的流行,不少初中学生在微信朋友圈忙着“发状态”,某校在使用微信的学生中随机抽取了部分,并调查他们平常每天上微信的时间,绘制了统计表和条形统计图:| 上微信的时间(小时) | 频数(人数) | 频率 |
| 0.5 | 38 | a |
| 1 | b | 0.25 |
| 1.5 | 14 | c |
| 2 | 8 | 0.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
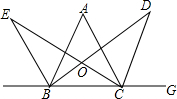 如图所示,在△ABC中,CD、BE是△ABC的外角平分线,BD为∠ABC的平分线,CE为∠ACB的平分线,BE、CE交于点E,BD、CD交于点D,试探索∠D与∠E的关系.
如图所示,在△ABC中,CD、BE是△ABC的外角平分线,BD为∠ABC的平分线,CE为∠ACB的平分线,BE、CE交于点E,BD、CD交于点D,试探索∠D与∠E的关系.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
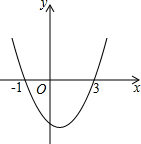 已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0),对于下列结论不正确的是( )
已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0),对于下列结论不正确的是( )| A. | b2-4ac>0 | B. | b+2a=0 | C. | abc>0 | D. | 8a+c<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
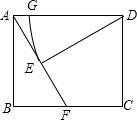 如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E.
如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
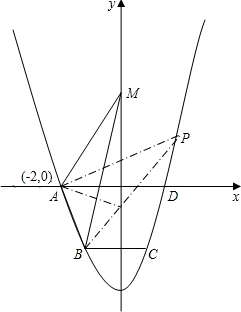 如图,抛物线y=ax2+c(a>0)经过梯形ABCD的四个顶点,梯形的底AD在x轴上,A点到原点的距离为2,梯形的高为3,C点到y轴的距离为1,
如图,抛物线y=ax2+c(a>0)经过梯形ABCD的四个顶点,梯形的底AD在x轴上,A点到原点的距离为2,梯形的高为3,C点到y轴的距离为1,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com