
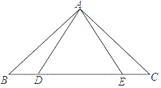
【题目】如图,在△ABC中,∠B=∠C=40°,BD=CE.
(1)求证:△ABE≌△ACD;
(2)若AB=BE,求∠DAE的度数.
【答案】(1)详见解析;(2)40°.
【解析】
(1)由题意得BD=CE,得出BE=CD,证出AB=AC,由SAS证明△ABE≌△ACD即可;
(2)由等腰三角形的性质和三角形内角和定理求出∠BEA=∠EAB=70°,证出AC=CD,由等腰三角形的性质得出∠ADC=∠DAC=70°,即可得出∠DAE的度数;
解:(1)∵BD=CE,
∴BCBD=BCCE,即BE=CD,
∵∠B=∠C=40°,
∴AB=AC,
在△ABE和△ACD中,
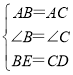 ,
,
∴△ABE≌△ACD(SAS);
(2)∵∠B=∠C=40°,AB=BE,
∴∠BEA=∠EAB=![]() (180°40°)=70°,
(180°40°)=70°,
∵BE=CD,AB=AC,
∴AC=CD,
∴∠ADC=∠DAC=![]() (180°40°)=70°,
(180°40°)=70°,
∴∠DAE=180°∠ADC∠BEA=180°70°70°=40°;


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:
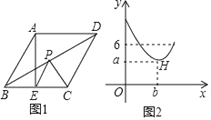
【题目】如图1,在菱形ABCD中,∠A=120°,点E是BC边的中点,点P是对角线BD上一动点,设PD的长度为x,PE与PC的长度和为y,图2是y关于x的函数图象,其中H是图象上的最低点,则a+b的值为( )
A.7![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
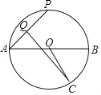
【题目】如图,AB为⊙O的直径,C为⊙O上一点,其中AB=4,∠AOC=120°,P为⊙O上的动点,连AP,取AP中点Q,连CQ,则线段CQ的最大值为( )
A. 3 B. 1+![]() C. 1+3
C. 1+3![]() D. 1+
D. 1+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
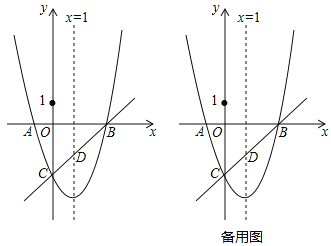
【题目】已知抛物线![]() 与x轴交于点A、B两点(A点在B点左侧),与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.
与x轴交于点A、B两点(A点在B点左侧),与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.
(1)求出抛物线的函数表达式;
(2)设点E时抛物线上一点,且S△ABE=![]() S△ABC,求tan∠ECO的值;
S△ABC,求tan∠ECO的值;
(3)点P在抛物线上,点Q在抛物线对称轴上,若以B、C、P、Q为顶点的四边形是平行四边形,求点P坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
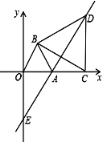
【题目】在直角坐标系中,O为坐标原点,点A坐标为(2,0),以OA为边在第一象限内作等边△OAB,C为x轴正半轴上的一个动点(OC>2),连接BC,以BC为边在第一象限内作等边△BCD,直线DA交y轴于E点.
(1)求证:△OBC≌△ABD
(2)随着C点的变化,直线AE的位置变化吗?若变化,请说明理由;若不变,请求出直线AE的解析式.
(3)以线段BC为直径作圆,圆心为点F,当C点运动到何处时,直线EF∥直线BO;这时⊙F和直线BO的位置关系如何?请给予说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 上有两点M(m+1,a)、N(m,b).
上有两点M(m+1,a)、N(m,b).
(1)当a=-1,m=1时,求抛物线![]() 的解析式;
的解析式;
(2)用含a、m的代数式表示b和c;
(3)当a<0时,抛物线![]() 满足
满足![]() ,
,![]() ,
,![]() ,
,
求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载,某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD的长等于24米,在l上点D的同侧取点A、B,使∠CAD=30°,∠CBD=60°.
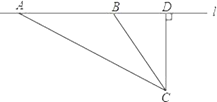
(1)求AB的长(结果保留根号);
(2)已知本路段对校车限速为45千米/小时,若测得某辆校车从A到B用时2秒,这辆校车是否超速?说明理由.(参考数据:![]() ≈1.7,
≈1.7,![]() ≈1.4)
≈1.4)
查看答案和解析>>
科目:初中数学 来源: 题型:
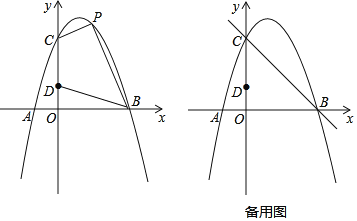
【题目】如图,对称轴为直线x=1的抛物线经过A(﹣1,0)、C(0,3)两点,与x轴的另一个交点为B,点D在y轴上,且OB=3OD
(1)求该抛物线的表达式;
(2)设该抛物线上的一个动点P的横坐标为t
①当0<t<3时,求四边形CDBP的面积S与t的函数关系式,并求出S的最大值;
②点Q在直线BC上,若以CD为边,点C、D、Q、P为顶点的四边形是平行四边形,请求出所有符合条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
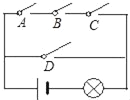
【题目】如图.电路图上有四个开关A、B、C、D和一个小灯泡,闭合开关D或同时闭合开关A,B,C都可使小灯泡发光.
(1)任意闭合其中一个开关,则小灯泡发光的概率等于 ;
(2)任意闭合其中两个开关,请用画树状图或列表的方法求出小灯泡发光的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com