
����Ŀ��У����ȫ�ǽ���������ע���ش����⣬��ȫ������Ҫ�dz��ٺͳ��أ�ij��ѧ��ѧ�С����������¼�·����ʻ�������ٶȵ�ʵ�飺���ڹ�·�Ա�ѡȡһ��C�����ڱ�ֱ�ij���l��ȷ����D��ʹCD��l��ֱ�����CD�ij�����24�ף���l�ϵ�D��ͬ��ȡ��A��B��ʹ��CAD��30������CBD��60����
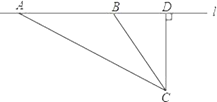
��1����AB�ij�������������ţ���
��2����֪��·�ζ�У������Ϊ45ǧ��/Сʱ�������ij��У����A��B��ʱ2�룬����У���Ƿ��٣�˵�����ɣ����ο����ݣ�![]() ��1.7��
��1.7��![]() ��1.4��
��1.4��
���𰸡���1��AB��16![]() �ף���2����У����AB·�γ��٣�
�ף���2����У����AB·�γ��٣�
��������
��1���ֱ���Rt��ADC��Rt��BDC��ͨ����������Ǻ������AD,BD�ij���Ȼ����AB��
��2����AB��������ʱ�����У�����ٶȣ�����45ǧ��/Сʱ���Ƚϼ���.
�⣺��1��������ã���Rt��ADC�У�tan30����![]() ��
��
���AD��![]() ��
��
��Rt��BDC ��tan60����![]() ��
��
���BD��![]() ,
,
����AB��AD��BD��![]() ���ף���
���ף���
��2��������A��B��ʱ2�룬�����ٶ�Ϊ![]() ��13.6����/�룩��
��13.6����/�룩��
��Ϊ13.6����/�룩��48.96ǧ��/Сʱ��45ǧ��/Сʱ
���Դ�У����AB·�γ��٣�


 ���Ǽ���С����ϵ�д�
���Ǽ���С����ϵ�д� �Ͻ�ƽ���Ȿϵ�д�
�Ͻ�ƽ���Ȿϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
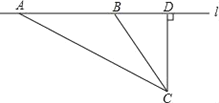
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�ֱ��y��x��1��������y����x2+bx+c����A��B���㣬����A��m��0����B��4��n��������������y�ύ�ڵ�C����x�ύ����һ��D��
��1����m��n��ֵ���������ߵĽ���ʽ��
��2����ͼ2������PΪ�߶�AD�ϵ�һ���㣨����A��D�غϣ����ֱ���AP��DPΪб�ߣ���ֱ��AD��ͬ��������ֱ����APM�͵���ֱ����DPN������MN����ȷ����MPN������ʱP������ꣻ
��3����ͼ3������BD��CD�����߶�CD���Ƿ���ڵ�Q��ʹ����A��D��QΪ���������������ABD���ƣ������ڣ���ֱ��д����Q�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����мƻ���ij��ľ�������ˮ�ܵ����и��죮�ù������ɼӵ���ʩ��ǡ���ڹ涨ʱ������ɣ������Ҷӵ���ʩ��������ɹ������������ǹ涨������1.5��������ɼס��������Ⱥ���10�죬��ô���µĹ������Ҷӵ�����ɻ���5�죮
��1������̵Ĺ涨ʱ���Ƕ����죿
��2����֪��ÿ���ʩ������Ϊ6500Ԫ���Ҷ�ÿ���ʩ������Ϊ3500Ԫ��Ϊ�����̹����Լ��ٶԾ�����ˮ��Ӱ�죬����ָ�Ӳ����վ����ù����ɼס������Ӻ�������ɣ���ù���ʩ�������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
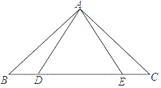
����Ŀ����ͼ���ڡ�ABC�У���B����C��40�㣬BD=CE��
(1)��֤����ABE�ա�ACD��
(2)��AB��BE�����DAE�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪ƽ���ı���ABCD�У�AE��BC�ڵ�E���Ե�BΪ���ģ�ȡ��ת�ǵ��ڡ�ABC���ѡ�BAE˳ʱ����ת���õ���BA��E�䣬����DA������ADC=60�㣬��ADA��=45�㣬���DA��E��=______�ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2015��2��28�գ�ǰ����֪�����߲��Ƴ��˹��������ļ�¼Ƭ������֮�¡��������˼���ķ��죮ij�����Ӵ���������������ȣ�2015���һ����Ͷ���ʽ�![]() ��Ԫ���ڶ����Ⱥ͵������ȼƻ���Ͷ���ʽ�
��Ԫ���ڶ����Ⱥ͵������ȼƻ���Ͷ���ʽ�![]() ��Ԫ�������������ȼƻ�Ͷ���ʽ��ƽ�������ʣ������������ȼƻ�Ͷ���ʽ��ƽ��������Ϊ
��Ԫ�������������ȼƻ�Ͷ���ʽ��ƽ�������ʣ������������ȼƻ�Ͷ���ʽ��ƽ��������Ϊ![]() ������������з���Ϊ__________.
������������з���Ϊ__________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
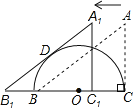
����Ŀ����ͼ����ABC�У���ACB��90����AB��5��AC��3��BCΪ��ԲO��ֱ��������ABC������CB����ƽ�Ƶõ���A1B1C1����A1B1���ԲO�����ڵ�Dʱ��ƽ�Ƶľ���ij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
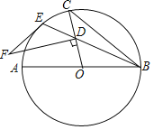
����Ŀ����ͼ��AB����O��ֱ����BE���ң���D����BE��һ�㣬����OD���ӳ�����O�ڵ�C������BC���ڹ���D��ֱ��OC��ֱ����ȡ��F��ʹ��DFE��2��CBE��
��1����˵��EF����O�����ߣ�
��2������O�İ뾶��6����D��OC���е㣬��CBE��15�㣬���߶�EF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��D��E�ֱ�����ABC�ı�AB��AC���е㣬H��G�DZ�BC�ϵĵ㣬��HG��![]() BC��S��ABC��24����ͼ����Ӱ���ֵ����Ϊ��������
BC��S��ABC��24����ͼ����Ӱ���ֵ����Ϊ��������

A. 4B. 6C. 8D. 12
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com