
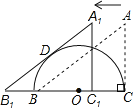
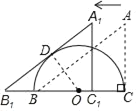
【题目】如图,△ABC中,∠ACB=90°,AB=5,AC=3,BC为半圆O的直径,将△ABC沿射线CB方向平移得到△A1B1C1.当A1B1与半圆O相切于点D时,平移的距离的长为_____.
【答案】![]()
【解析】
连结OG,如图,根据勾股定理得到BC=4,根据平移的性质得到CC1=BB1,A1C1=AC=3,A1B1=AB=5,∠A1C1B1=∠ACB=90°,根据切线的性质得到OD⊥A1B1,根据相似三角形的性质即可得到结论.
连结OG,如图,
∵∠BAC=90°,AB=5,AC=3,
∴BC=![]() =4,
=4,
∵Rt△ABC沿射线CB方向平移,当A1B1与半圆O相切于点D,得△A1B1C1,
∴CC1=BB1,A1C1=AC=3,A1B1=AB=5,∠A1C1B1=∠ACB=90°,
∵A1B1与半圆O相切于点D,
∴OD⊥A1B1,
∵BC=4,线段BC为半圆O的直径,
∴OB=OC=2,
∵∠GEO=∠DEF,
∴Rt△B1OD∽Rt△B1A1C1,
∴![]() ,即
,即![]() ,解得OB1=
,解得OB1=![]() ,
,
∴BB1=OB1﹣OB=![]() ﹣2=
﹣2=![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
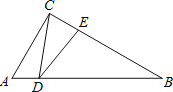
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=2,D是AB边上一个动点(不与点A、B重合),E是BC边上一点,且∠CDE=30°.设AD=x,BE=y,则下列图象中,能表示y与x的函数关系的图象大致是( )
A.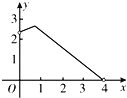 B.
B.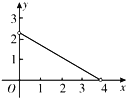 C.
C.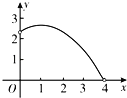 D.
D.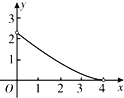
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一期间,某商场计划购进甲、乙两种商品,已知购进甲商品1件和乙商品3件共需240元;购进甲商品2件和乙商品1件共需130元.
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
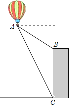
【题目】如图,热气球的探测器显示,从热气球A看一栋大楼顶部B的俯角为![]() ,看这栋大楼底部C的俯角为
,看这栋大楼底部C的俯角为![]() ,热气球A的高度为270米,则这栋大楼的高度为______米
,热气球A的高度为270米,则这栋大楼的高度为______米![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
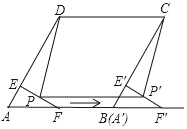
【题目】如图,在菱形ABCD中,∠A=60°,AD=4,点F是AB的中点,过点F作FE⊥AD,垂足为E,将△AEF沿点A到点B的方向平移,得到△A'E'F',设点P、P'分别是EF、E'F'的中点,当点A'与点B重合时,四边形PP'CD的面积为( )
A. 7![]() B. 6
B. 6![]() C. 8
C. 8![]() D. 8
D. 8![]() ﹣4
﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用2500元购进A、B两种新型节能台灯共50盏,这两种台灯的进价、标价如下表所示.
类型 价格 | A型 | B型 |
进价(元/盏) | 40 | 65 |
标价(元/盏) | 60 | 100 |
(1)这两种台灯各购进多少盏?
(2)在每种台灯销售利润不变的情况下,若该商场计划销售这批台灯的总利润至少为1400元,问至少需购进B种台灯多少盏?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知反比例函数y=![]() 的图象经过点A(1,
的图象经过点A(1,![]() ).
).
(1)试确定此反比例函数的解析式;
(2)点O是坐标原点,将线OA绕O点顺时针旋转30°得到线段OB,判断点B是否在此反比例函数的图象上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B在反比例函数![]() 的图象上,点C,D在反比例函数
的图象上,点C,D在反比例函数![]() 的图象上,AC//BD//y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为
的图象上,AC//BD//y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为![]() ,则k的值为( )
,则k的值为( )

A. 4 B. 3 C. 2 D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com