
【题目】在平面直角坐标系中,已知反比例函数y=![]() 的图象经过点A(1,
的图象经过点A(1,![]() ).
).
(1)试确定此反比例函数的解析式;
(2)点O是坐标原点,将线OA绕O点顺时针旋转30°得到线段OB,判断点B是否在此反比例函数的图象上,并说明理由.
【答案】(1)y=![]() ;(2)在,理由见解析
;(2)在,理由见解析
【解析】
(1)把点A坐标代入反比例函数解析式,求出k值即可;(2)过点A作x轴的垂线交x轴于点C.过点B作x轴的垂线交x轴于点D.利用勾股定理可求出OA的长,进而可得∠OAC=30°,∠AOC=60°,由旋转的性质可得∠AOB=30°,即可求出∠BOD的度数,进而可得BD、OD的长,即可得B点坐标,把B点横坐标代入解析式即可得答案.
(1)把A(1,![]() )代入y=
)代入y=![]() ,得k=1×
,得k=1×![]() =
=![]() ,
,
∴反比例函数的解析式为y=![]() .
.
(2)过点A作x轴的垂线交x轴于点C.
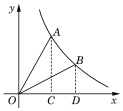
在Rt△AOC中,OC=1,AC=![]() .
.
由勾股定理,得OA=![]() =2,
=2,
∴∠OAC=30°,∠AOC=60°.
过点B作x轴的垂线交x轴于点D.
由题意,∠AOB=30°,OB=OA=2,
∴∠BOD=30°,
在Rt△BOD中,得BD=1,OD=![]() ,
,
∴B点坐标为(![]() ,1).
,1).
将x=![]() 代入y=
代入y=![]() 中,得y=1,
中,得y=1,
∴点B(![]() ,1)在反比例函数y=
,1)在反比例函数y=![]() 的图象上.
的图象上.


科目:初中数学 来源: 题型:
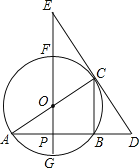
【题目】如图,⊙O中,FG、AC是直径,AB是弦,FG⊥AB,垂足为点P,过点C的直线交AB的延长线于点D,交GF的延长线于点E,已知AB=4,⊙O的半径为![]() .
.
(1)分别求出线段AP、CB的长;
(2)如果OE=5,求证:DE是⊙O的切线;
(3)如果tan∠E=![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的顶点坐标为A(﹣4,1),B(﹣2,3),C(﹣1,2).
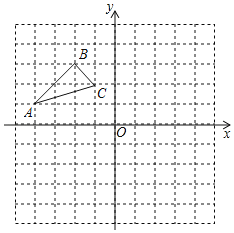
(1)画出△ABC关于原点O成中心对称的△A′B′C′,点A′,B′,C′分别是点A,B,C的对应点.
(2)求过点B′的反比例函数解析式.
(3)判断A′B′的中点P是否在(2)的函数图象上.
查看答案和解析>>
科目:初中数学 来源: 题型:
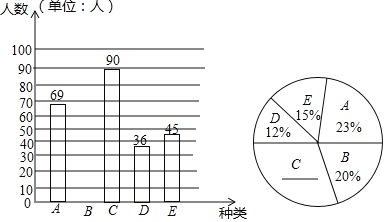
【题目】某中学为了了解在校学生对校本课程的喜爱情况,随机调查了九年级学生对A,B,C,D,E五类校本课程的喜爱情况,要求每位学生只能选择一类最喜欢的校本课程,根据调查结果绘制了如下的两个统计图.
请根据图中所提供的信息,完成下列问题:
(1)本次被调查的学生的人数为 ;
(2)补全条形统计图;
(3)扇形统计图中,C类所在扇形的圆心角的度数为 ;
(4)若该中学有4000名学生,请估计该校喜爱C,D两类校本课程的学生共有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
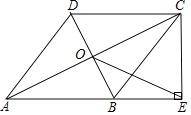
【题目】如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若AB=![]() ,BD=2,求OE的长.
,BD=2,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,⊙O的半径为r(r>0).给出如下定义:若平面上一点P到圆心O的距离d,满足![]() ,则称点P为⊙O的“随心点”.
,则称点P为⊙O的“随心点”.
(1)当⊙O的半径r=2时,A(3,0),B(0,4),C(![]() ,2),D(
,2),D(![]() ,
,![]() )中,⊙O的“随心点”是 ;
)中,⊙O的“随心点”是 ;
(2)若点E(4,3)是⊙O的“随心点”,求⊙O的半径r的取值范围;
(3)当⊙O的半径r=2时,直线y=- x+b(b≠0)与x轴交于点M,与y轴交于点N,若线段MN上存在⊙O的“随心点”,直接写出b的取值范围 .
查看答案和解析>>
科目:初中数学 来源: 题型:
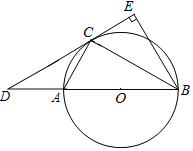
【题目】如图,AB是⊙O的直径,点C在圆O上,BE⊥CD垂足为E,CB平分∠ABE,连接BC
(1)求证:CD为⊙O的切线;
(2)若cos∠CAB=![]() ,CE=
,CE=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
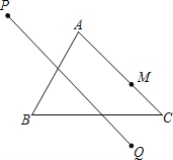
【题目】如图,在△ABC中,∠A=75°,∠C=45°,BC=4,点M是AC边上的动点,点M关于直线AB、BC的对称点分别为P、Q,则线段PQ长的取值范围是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com