
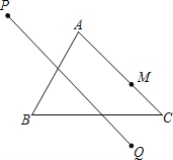
【题目】如图,在△ABC中,∠A=75°,∠C=45°,BC=4,点M是AC边上的动点,点M关于直线AB、BC的对称点分别为P、Q,则线段PQ长的取值范围是______.
【答案】2![]() ≤PQ≤4
≤PQ≤4![]()
【解析】
根据题意连接BP、BQ、BM,过点B作BD⊥PQ于点D,由对称性可知PB=BM=BQ、△PBQ为等腰三角形,进而即可得出PD=![]() PB,再根据BM的取值范围即可得出线段PQ长的取值范围.
PB,再根据BM的取值范围即可得出线段PQ长的取值范围.
解:∵∠A=75°,∠C=45°,
∴∠ABC=180°-75°-45°=60°,
连接BP、BQ、BM,过点B作BD⊥PQ于点D,如图所示.
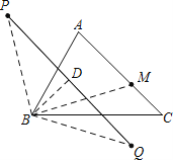
∵点M关于直线AB、BC的对称点分别为P、Q,
∴BP=BQ=BM,∠PBA=∠MBA,∠MBC=∠QBC,
∴∠PBQ=120°,
∵PB=BQ,
∴∠BPQ=∠BQP=30°,
∴cos30°=![]() =
=![]() ,
,
∴PD=![]() PB,
PB,
∵BC=4,∠C=45°,
∴2![]() ≤BM≤4,
≤BM≤4,
∵BM=PB,
∴2![]() ≤PB≤4,
≤PB≤4,
∴2![]() ≤PD≤4×
≤PD≤4×![]() ,即
,即![]() ≤PD≤2
≤PD≤2![]() ,
,
∵PQ=2PD,
∴2![]() ≤PQ≤4
≤PQ≤4![]() .
.
故答案为:2![]() ≤PQ≤4
≤PQ≤4![]() .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知反比例函数y=![]() 的图象经过点A(1,
的图象经过点A(1,![]() ).
).
(1)试确定此反比例函数的解析式;
(2)点O是坐标原点,将线OA绕O点顺时针旋转30°得到线段OB,判断点B是否在此反比例函数的图象上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批名牌衬衫,平均每天可售出![]() 件,每件盈利
件,每件盈利![]() 元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衫每降价
元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衫每降价![]() 元,商场平均每天可多售出
元,商场平均每天可多售出![]() 件,若商场平均每天要盈利
件,若商场平均每天要盈利![]() 元,每件衬衫应降价多少元?
元,每件衬衫应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中任选两个作为补充条件,使ABCD为正方形.现有下列四种选法,你认为其中错误的是( )
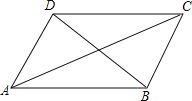
A.②③B.①③C.①②D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形 ABCD 中,AB=8,BC=4.点 E 在边 AB 上,点 F 在边 CD 上,点 G、H 在对角线 AC 上.若四边形 EGFH 是菱形,则 AE 的长是( )
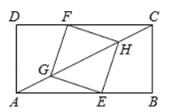
A.2B.3C.5D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂家销售一种产品,现准备从网上销售和市场直销两种销售方案中选择一种进行销售.由于受各种不确定因素影响,不同销售的方案会产生不同的成本和其它费用.设每月销售x件,网上销售月利润为w网(元),市场直销月利润为w市(元),具体信息如表:
每件售价(元) | 每件成本(元) | 月其他费用(元) | |
网上销售 | - | 20 | 45000 |
市场直销 | 120 | k |
|
其中k为常数,且30≤k≤50.月利润=月销售额-月成本-月其它费用.
(1)当x=500时,网上销售单价为______元.
(2)分别求出w网,w市与x间的函数解析式(不必写x的取值范围).
(3)若网上销售月利润的最大值与市场直销月利润的最大值相同,求k的值.
(4)如果某月要将3000件产品全部销售完,请你通过分析帮厂家做出决策,选择在网上销售还是市场直销才能使月利润较大?
查看答案和解析>>
科目:初中数学 来源: 题型:
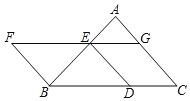
【题目】如图,以BC为底边的等腰△ABC,点D,E,G分别在BC,AB,AC上,且EG∥BC,DE∥AC,延长GE至点F,使得BE=BF.
(1)求证:四边形BDEF为平行四边形;
(2)当∠C=30°,![]() 时,求D,F两点间的距离.
时,求D,F两点间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司计划购买A,B两种型号的机器人搬运材料.已知A型机器人比B型机器人每小时多搬运30kg材料,且A型机器人搬运1000kg材料所用的时间与B型机器人搬运800kg材料所用的时间相同.
(1)求A,B两种型号的机器人每小时分别搬运多少材料;
(2)该公司计划采购A,B两种型号的机器人共20台,要求每小时搬运材料不得少于2800kg,则至少购进A型机器人多少台?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com