
【题目】如图,矩形 ABCD 中,AB=8,BC=4.点 E 在边 AB 上,点 F 在边 CD 上,点 G、H 在对角线 AC 上.若四边形 EGFH 是菱形,则 AE 的长是( )
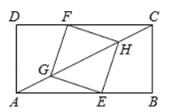
A.2B.3C.5D.6
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
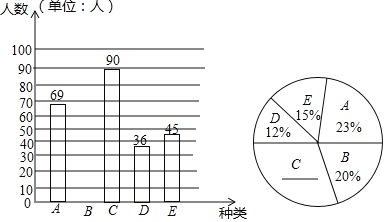
【题目】某中学为了了解在校学生对校本课程的喜爱情况,随机调查了九年级学生对A,B,C,D,E五类校本课程的喜爱情况,要求每位学生只能选择一类最喜欢的校本课程,根据调查结果绘制了如下的两个统计图.
请根据图中所提供的信息,完成下列问题:
(1)本次被调查的学生的人数为 ;
(2)补全条形统计图;
(3)扇形统计图中,C类所在扇形的圆心角的度数为 ;
(4)若该中学有4000名学生,请估计该校喜爱C,D两类校本课程的学生共有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 两条对角线
两条对角线![]() 、
、![]() 交于
交于![]() ,过
,过![]() 任作一直线
任作一直线![]() 与边
与边![]() ,
,![]() 交于
交于![]() ,
,![]() ,
,![]() 的垂直平分线与边
的垂直平分线与边![]() ,
,![]() 交于
交于![]() ,
,![]() .设正方形
.设正方形![]() 的面积为
的面积为![]() ,四边形
,四边形![]() 的面积为
的面积为![]() .
.
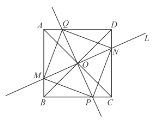
(1)求证:四边形![]() 是正方形;
是正方形;
(2)若![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“普洱茶”是云南有名的特产,某网店专门销售某种品牌的普洱茶,成本为30元/盒,每天销售![]() (件)与销售单价
(件)与销售单价![]() (元)之间存在一次函数关系,如图所示.
(元)之间存在一次函数关系,如图所示.
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)如果规定每天该种普洱茶的销售量不低于240盒,该网店店主热心公益事业,决定从每天的销售利润中捐出500元给扶贫基金会,当销售单价为多少元时,每天获取的净利润最大,最大净利润是多少?(注:净利润=总利润-捐款)
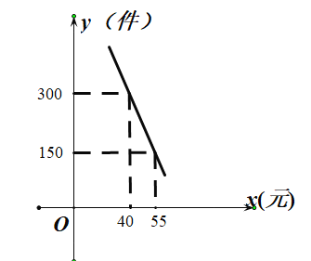
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.已知:AB![]() , CD
, CD![]() .
.
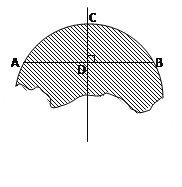
(1)求作此残片所在的圆(不写作法,保留作图痕迹)
(2)求(1)中所作圆的半径
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=75°,∠C=45°,BC=4,点M是AC边上的动点,点M关于直线AB、BC的对称点分别为P、Q,则线段PQ长的取值范围是______.
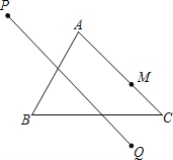
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=﹣2x+4分别交x轴、y轴于点A、B.抛物线过A、B两点,点P是线段AB上一动点,过点P作PC⊥x轴于点C,交抛物线于点D.
(1)如图1,设抛物线顶点为M,且M的坐标是(![]() ,
,![]() ),对称轴交AB于点N.
),对称轴交AB于点N.
①求抛物线的解析式;
②是否存在点P,使四边形MNPD为菱形?并说明理由;
(2)是否存在这样的点D,使得四边形BOAD的面积最大?若存在,求出此时点D的坐标;若不存在,请说明理由.
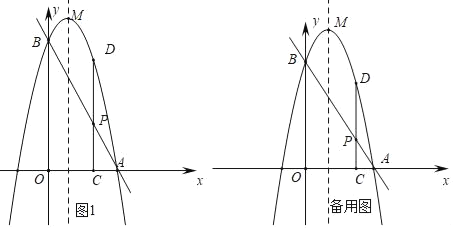
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在兰州市开展的“体育、艺术2+1”活动中,某校根据实际情况,决定主要开设A:乒
乓球,B:篮球,C:跑步,D:跳绳这四种运动项目.为了解学生喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如下的条形统计图和扇形统计图.请你结合图中信息解答下列问题:
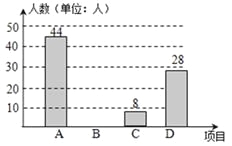
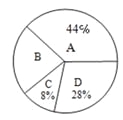
(1)样本中喜欢B项目的人数百分比是 ,其所在扇形统计图中的圆心角的度数是 ;
(2)把条形统计图补充完整;
(3)已知该校有1000人,根据样本估计全校喜欢乒乓球的人数是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com