
����Ŀ����ƽ��ֱ������ϵxOy�У���O�İ뾶Ϊr��r��0�����������¶��壺��ƽ����һ��P��Բ��O�ľ���d������![]() ����Ƶ�PΪ��O�������ĵ�����
����Ƶ�PΪ��O�������ĵ�����
��1������O�İ뾶r=2ʱ��A��3��0����B��0��4����C��![]() ��2����D��
��2����D��![]() ��
��![]() ���У���O�������ĵ����� ��
���У���O�������ĵ����� ��
��2������E��4��3���ǡ�O�������ĵ��������O�İ뾶r��ȡֵ��Χ��
��3������O�İ뾶r=2ʱ��ֱ��y=- x+b��b��0����x�ύ�ڵ�M����y�ύ�ڵ�N�����߶�MN�ϴ��ڡ�O�������ĵ�����ֱ��д��b��ȡֵ��Χ ��
���𰸡�(1) A,C ����2��![]() ��(3) 1��b��
��(3) 1��b��![]() ��-
��-![]() ��b��-1��
��b��-1��
��������
��1��������֪�������d�ķ�Χ��1��d��3���ٽ��������O��ľ��룬�����ж��Ƿ��ڴ˷�Χ�ڼ��ɣ����������ļ�Ϊ���ĵ㣻
��2�����ݵ�E��4��3���ǡ�O�������ĵ������ɸ���![]() �����d=5�������r�ķ�Χ���ɣ�
�����d=5�������r�ķ�Χ���ɣ�
��3����ͼa��b��c��d����O�İ뾶r=2��������ĵ㷶Χ![]() ���ٷ������N��y��������ʱ������N��y�Ḻ����ʱ����������ۼ���.
���ٷ������N��y��������ʱ������N��y�Ḻ����ʱ����������ۼ���.
(1) �ߡ�O�İ뾶r=2��
��![]() =3��
=3��![]() =1
=1
��1��d��3
��A��3��0����
��OA=3���ڷ�Χ��
���A�ǡ�O�������ĵ���
��B��0��4��
��OB=4����4��3�����ڷ�Χ��
��B�Dz��ǡ�O�������ĵ�����
��C��![]() ��2����
��2����
��OC=![]() ���ڷ�Χ��
���ڷ�Χ��
���C�ǡ�O�������ĵ�����
��D��![]() ��
��![]() ����
����
��OD=![]() ��1�����ڷ�Χ��
��1�����ڷ�Χ��
���D���ǡ�O�������ĵ�����
�ʴ�Ϊ��A,C
��2���ߵ�E��4��3���ǡ�O�������ĵ���
��OE=5����d=5
��![]() �� ��r=10
�� ��r=10
�� ![]() ��
��![]()
��![]()
(3)
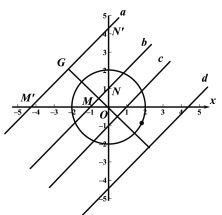
����ͼa��b��c��d����O�İ뾶r=2�����ĵ㷶Χ![]()
��![]()
��ֱ��MN�Ľ���ʽΪy=x+b��
��OM=ON��
�ٵ�N��y��������ʱ��
����M�ǡ�O�������ĵ�������ʱ����M��-1��0����
��M��-1��0������ֱ��MN�Ľ���ʽy=x+b�У���ã�b=1��
����b����СֵΪ1��
����O��OG��M'N'��G��
����G�ǡ�O�������ĵ���ʱ����ʱOG=3��
��Rt��ON'G����ON'G=45����
��GO=3
����Rt��GNN����![]() =
=![]() =
=![]() =
=![]() ��
��
b�����ֵΪ![]() ��
��
��1��b��![]() ��
��
�ڵ���N��y�Ḻ����ʱ��ͬ�ٵķ����ó�-![]() ��b��-1��
��b��-1��
����������b��ȡֵ��Χ�ǣ�1��b��![]() ��-
��-![]() ��b��-1��
��b��-1��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���![]() (
(![]() Ϊ����)�����Ա���
Ϊ����)�����Ա���![]() ��ֵ����
��ֵ����![]() ʱ�����Ӧ�ĺ���ֵ
ʱ�����Ӧ�ĺ���ֵ![]() �����ֵΪ
�����ֵΪ![]() ,��
,��![]() ��ֵΪ �� ��
��ֵΪ �� ��
A.2��4B.0��-4C.2��-4D.0��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ɽ�����ڼ䣬���ֳ�Ͷ��150��Ԫ����һ�����������ʩ��������ά�ޱ������ã�Ԥ�ƿ��ź�ÿ�¿ɴ���31��Ԫ���������ֳ����źӵ�1���µ���x���µ�ά�ޱ��������ۼ�Ϊy(��Ԫ)����y��ax2��bx���������տ۳�Ͷ�ʺ�ά�ޱ������ó�Ϊ���ֳ��Ĵ�����g(��Ԫ)��gҲ�ǹ���x�Ķ��κ�����
(1)��ά�ޱ������õ�1����Ϊ2��Ԫ����2����Ϊ4��Ԫ����y����x�Ľ���ʽ��
(2)������g����x�Ľ���ʽ��
(3)����ʩ���ż����º����ֳ��Ĵ�����ﵽ������������森
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���֪����������y��![]() ��ͼ����A(1��
��ͼ����A(1��![]() )��
)��
(1)��ȷ���˷����������Ľ���ʽ��
(2)��O������ԭ�㣬����OA��O��˳ʱ����ת30���õ��߶�OB���жϵ�B�Ƿ��ڴ˷�����������ͼ���ϣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ![]() �У�ֱ��
�У�ֱ��![]() �뺯��
�뺯��![]() ��ͼ����
��ͼ����![]() ��
��![]() ���㣬�ҵ�
���㣬�ҵ�![]() ������Ϊ
������Ϊ![]() ��
��
��1����![]() ��ֵ��
��ֵ��
��2����֪��![]() ������
������![]() ��ƽ����
��ƽ����![]() ���ֱ�ߣ���ֱ��
���ֱ�ߣ���ֱ��![]() �ڵ�
�ڵ�![]() ��������
��������![]() ��ͼ���ڵ�
��ͼ���ڵ�![]() ��
��
�ٵ�![]() ʱ�����߶�
ʱ�����߶�![]() �ij���
�ij���
����![]() ����Ϻ�����ͼ��ֱ��д��
����Ϻ�����ͼ��ֱ��д��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
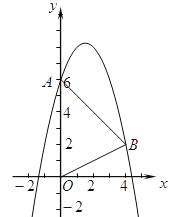
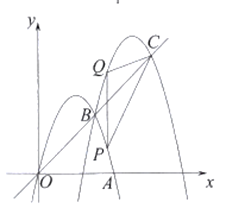
����Ŀ����ͼ��������![]() ����
����![]() ��
��![]() ���㣮
���㣮
��1���������ߵĽ���ʽ��
��2��������������ƽ��![]() ����λ��ʹƽ�ƺ�õ��������߶�������
����λ��ʹƽ�ƺ�õ��������߶�������![]() ���ڲ���������
���ڲ���������![]() �ı߽磩����
�ı߽磩����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3����![]() ����������һ���㣬�Ƿ���ڵ�
����������һ���㣬�Ƿ���ڵ�![]() ��ʹ
��ʹ![]() �������
�������![]() �������ڣ�ֱ��д��P�����ꣻ�������ڣ���˵�����ɣ�
�������ڣ�ֱ��д��P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��
��![]() ���������ڵ�
���������ڵ�![]() ��������
��������![]() ƽ�Ƶõ�������
ƽ�Ƶõ�������![]() ��
��![]() ���ڵ�
���ڵ�![]() ��ֱ��
��ֱ��![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() ����
����![]() ��
��
![]() ֱ��д����
ֱ��д����![]() ����
����![]() �����꣮
�����꣮![]() ��������
��������![]() �ı���ʽ��
�ı���ʽ��
![]() ��
��![]() ��������
��������![]() ��
��![]() ��--�㣬��
��--�㣬��![]() �ύ������
�ύ������![]() �ڵ�
�ڵ�![]() ������
������![]() �����
�����![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() ��
��![]() Ϊ��ֵʱ��ʹ
Ϊ��ֵʱ��ʹ![]() ��������������ֵ��
��������������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�����һ�����Ƴ�����ƽ��ÿ����۳�![]() ����ÿ��ӯ��
����ÿ��ӯ��![]() Ԫ��Ϊ���������ۣ�����ӯ����������ٿ�棬�̳�������ȡ�ʵ��Ľ��۴�ʩ�������鷢�֣����ÿ������ÿ����
Ԫ��Ϊ���������ۣ�����ӯ����������ٿ�棬�̳�������ȡ�ʵ��Ľ��۴�ʩ�������鷢�֣����ÿ������ÿ����![]() Ԫ���̳�ƽ��ÿ��ɶ��۳�
Ԫ���̳�ƽ��ÿ��ɶ��۳�![]() �������̳�ƽ��ÿ��Ҫӯ��
�������̳�ƽ��ÿ��Ҫӯ��![]() Ԫ��ÿ������Ӧ���۶���Ԫ��
Ԫ��ÿ������Ӧ���۶���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�ڽ��ڡ�O����I�ǡ�ABC�����ģ���AIC��124�㣬��E��AD���ӳ����ϣ����CDE�Ķ���Ϊ_____��
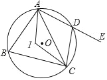
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com