
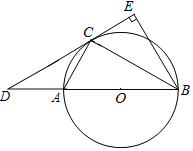
【题目】如图,AB是⊙O的直径,点C在圆O上,BE⊥CD垂足为E,CB平分∠ABE,连接BC
(1)求证:CD为⊙O的切线;
(2)若cos∠CAB=![]() ,CE=
,CE=![]() ,求AD的长.
,求AD的长.
【答案】(1)见解析;(2)AD=![]() .
.
【解析】
(1)连接OC,根据等边对等角,以及角平分线的定义,即可证得∠OCB=∠EBC,则OC∥BE,从而证得OC⊥CD,即CD是⊙O的切线;
(2)根据勾股定理和相似三角形的判定和性质即可得到结论.
证明:(1)连接OC.
∵OC=OB,
∴∠ABC=∠OCB,
又∵∠EBC=∠ABC,
∴∠OCB=∠EBC,
∴OC∥BE,
∵BE⊥CD,
∴OC⊥CD,
∴CD是⊙O的切线;
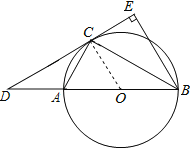
(2)设AB=x,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴直角△ABC中,AC=ABcos∠CAB=![]() ,
,
∴BC=![]() =
=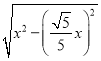 =
=![]() x,
x,
∵∠BCE+∠BCO=∠CAB+∠ABC=90°,
∵OC=OB,
∴∠OCB=∠OBC,
∴∠CAB=∠BCE,
∵∠E=∠ACB=90°,
∴△ACB∽△CEB,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴x=![]() ,
,
∴AB=![]() ,BC=5,
,BC=5,
∵△ACB∽△CEB,
∴∠CAB =∠ECB= cos∠CAB=![]()
∴BE=2![]() ,
,
∵OC∥BE,
∴△DOC∽△DBE,
∴![]() =
=![]() ,
,
∴![]() =
= ,
,
∴AD=![]() .
.



 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】扬州某风景区门票价格如图所示,有甲、乙两个旅行团队,计划在端午节期间到该景点游玩,两团队游客人数之和为100人,若乙团队人数不超过40人,甲团队人数不超过80人,设甲团队人数为![]() 人,如果甲、乙两团队分别购买门票,两团队门票款之和为
人,如果甲、乙两团队分别购买门票,两团队门票款之和为![]() 元.
元.
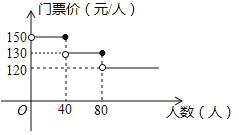
(1)直接写出![]() 关于
关于![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)计算甲、乙两团队联合购票比分别购票最多可节约多少钱?
(3)该景区每年11月、12月为淡季,景区决定在这两个月实行门票打五折的优惠(打折期间不售团体票),以吸引大量游客,提高景区收入;景区经过调研发现,随着接待游客数的增加,景区的运营成本也随之增加,景区运营成本![]() (万元)与两个月游客总人数
(万元)与两个月游客总人数![]() (万人)之间满足函数关系式:
(万人)之间满足函数关系式:![]() ;两个月游客总人数
;两个月游客总人数![]() (万人)满足:
(万人)满足:![]() ,且淡季每天游客数基本相同;为了获得最大利润,景区决定通过网络预约购票的方式控制淡季每天游客数,请问景区的决定是否正确?并说明理由.(利润
,且淡季每天游客数基本相同;为了获得最大利润,景区决定通过网络预约购票的方式控制淡季每天游客数,请问景区的决定是否正确?并说明理由.(利润![]() 门票收入
门票收入![]() 景区运营成本)
景区运营成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知反比例函数y=![]() 的图象经过点A(1,
的图象经过点A(1,![]() ).
).
(1)试确定此反比例函数的解析式;
(2)点O是坐标原点,将线OA绕O点顺时针旋转30°得到线段OB,判断点B是否在此反比例函数的图象上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
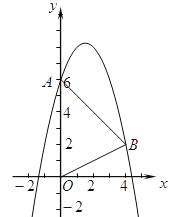
【题目】如图,抛物线![]() 经过
经过![]() 、
、![]() 两点.
两点.
(1)求抛物线的解析式;
(2)将抛物线向下平移![]() 个单位,使平移后得到的抛物线顶点落在
个单位,使平移后得到的抛物线顶点落在![]() 的内部(不包括
的内部(不包括![]() 的边界),求
的边界),求![]() 的取值范围.
的取值范围.
(3)若![]() 是抛物线上一动点,是否存在点
是抛物线上一动点,是否存在点![]() ,使
,使![]() 的面积是
的面积是![]() ?若存在,直接写出P点坐标;若不存在,请说明理由.
?若存在,直接写出P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
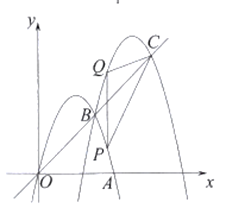
【题目】如图,抛物线![]() 交
交![]() 轴正半轴于点
轴正半轴于点![]() 将抛物线
将抛物线![]() 平移得到拋物线
平移得到拋物线![]() 与
与![]() 交于点
交于点![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,且
,且![]() .
.
![]() 直接写出点
直接写出点![]() ,点
,点![]() 的坐标.
的坐标.![]() 求抛物线
求抛物线![]() 的表达式.
的表达式.
![]() 点
点![]() 是抛物线
是抛物线![]() 上
上![]() 间--点,作
间--点,作![]() 轴交抛物线
轴交抛物线![]() 于点
于点![]() ,连结
,连结![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() 当
当![]() 为何值时,使
为何值时,使![]() 的面积最大,并求出最大值.
的面积最大,并求出最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅社有100张床位,若每张床位每晚收费100元,床位可全部租出,若每张床位每晚收费提高20元,则减少10张床位租出;若每张床位每晚收费再提高20元,则再减少10张床位租出.以每次提高20元的这种方法变化下去,为了投资少而收入最多,每张床位每晚应提高( )
A.60元B.50元C.40元D.40元或60元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批名牌衬衫,平均每天可售出![]() 件,每件盈利
件,每件盈利![]() 元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衫每降价
元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衫每降价![]() 元,商场平均每天可多售出
元,商场平均每天可多售出![]() 件,若商场平均每天要盈利
件,若商场平均每天要盈利![]() 元,每件衬衫应降价多少元?
元,每件衬衫应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中任选两个作为补充条件,使ABCD为正方形.现有下列四种选法,你认为其中错误的是( )
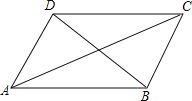
A.②③B.①③C.①②D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
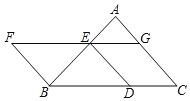
【题目】如图,以BC为底边的等腰△ABC,点D,E,G分别在BC,AB,AC上,且EG∥BC,DE∥AC,延长GE至点F,使得BE=BF.
(1)求证:四边形BDEF为平行四边形;
(2)当∠C=30°,![]() 时,求D,F两点间的距离.
时,求D,F两点间的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com